Imagining the 4th Dimension

Imagining the 4th Dimension

Imagining extra dimensions is a fantastic ToK topic – it is something which seems counter-intuitively false, something which we have no empirical evidence to support, and yet it is something which seems to fit the latest mathematical models on string theory (which requires 11 dimensions).  Mathematical models have consistently been shown to be accurate in describing reality, but when they predict a reality that is outside our realm of experience then what should we believe?  Our senses?  Our intuition?  Or the mathematical models?

Carl Sagan produced a great introduction to the idea of extra dimensions  based on the Flatland novel.  This imagines reality as experienced by two dimensional beings.

Mobius strips are a good gateway  into the weird world of topology – as they are 2D shapes with only 1 side.  There are some nice activities to do with Mobius strips – first take a pen and demonstrate that you can cover all of the strip without lifting the pen.  Next, cut along the middle of the strip and see the resulting shape.  Next start again with a new strip, but this time start cutting from nearer the edge (around 1/3 in).  In both cases have students predict what they think will happen.

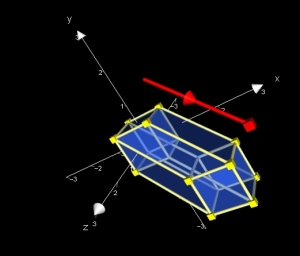
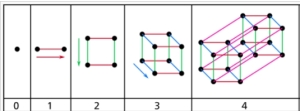
Next we can move onto the Hypercube (or Tesseract).  We can see an Autograph demonstration of what the fourth dimensional cube looks like here.

The page allows you to model 1, then 2, then 3 dimensional traces – each time representing a higher dimensional cube.

It’s also possible to create a 3 dimensional representation of a Tesseract using cocktail sticks – you simply need to make 2 cubes, and then connect one vertex in each cube to the other as in the diagram below:

For a more involved discussion (it gets quite involved!) on imagining extra dimensions, this 10 minute cartoon takes us through how to imagine 10 dimensions.

It might also be worth touching on why mathematicians believe there might be 11 dimensions.  Michio Kaku has a short video (with transcript) here and Brian Greene also has a number of good videos on the subject.

All of which brings us onto empirical testing – if a mathematical theory can not be empirically tested then does it differ from a belief?  Well, interestingly this theory can be tested – by looking for potential violations to the gravitational inverse square law.

The current theory expects that the extra dimensions are themselves incredibly small – and as such we would only notice their effects on an incredibly small scale.  The inverse square law which governs gravitational attraction between 2 objects would be violated on the microscopic level if there were extra dimensions – as the gravitational force would “leak out” into these other dimensions.  Currently physicists are carrying out these tests – and as yet no violation of the inverse square law has been found, but such a discovery would be one of the greatest scientific discoveries in history.

Other topics with counter-intuitive arguments about reality based on mathematical models are Nick Bostrom’s Computer Simulation Hypothesis, the Hologram Universe Hypothesis and Everett’s Many Worlds quantum mechanics interpretation.  I will blog more on these soon!

If you enjoyed this topic you may also like:

Wolf Goat Cabbage Space – a problem solved by 3d geometry.

Graham’s Number – a number literally big enough to collapse your head into a black hole.

Essential resources for IB students:

1) Exploration Guides and Paper 3 Resources

I’ve put together four comprehensive pdf guides to help students prepare for their exploration coursework and Paper 3 investigations. The exploration guides talk through the marking criteria, common student mistakes, excellent ideas for explorations, technology advice, modeling methods and a variety of statistical techniques with detailed explanations. I’ve also made 17 full investigation questions which are also excellent starting points for explorations.  The Exploration Guides can be downloaded here and the Paper 3 Questions can be downloaded here.