IB Maths Resources from Intermathematics
IB Maths Resources: 300 IB Maths Exploration ideas, video tutorials and Exploration Guides
The Riemann Sphere The Riemann Sphere is a fantastic glimpse of where geometry can take you when you escape from the constraints of Euclidean Geometry - the geometry of circles and lines taught at school. Riemann, the German 19th Century mathematician, devised a way of representing every point on a plane as a point on... Continue Reading →
Divisibility tests allow us to calculate whether a number can be divided by another number. For example, can 354 be divided by 3? Can 247,742 be divided by 11? So what are the rules behind divisibility tests, and more interestingly, how can we prove them? Divisibility rule for 3 The most well known divisibility rule... Continue Reading →
In sports leagues around the world, managers are often only a few bad results away from the sack - but is this all down to a misunderstanding of statistics? According to the Guardian, in the 21 year history of the Premier League, approximately 140 managers have been sacked. In more recent years the job is... Continue Reading →
The Battle over Homework: Marking in Mathematics Within five minutes of any teaching inspection from OFSTED, the inspector will be leafing through students’ exercise books in search of evidence of regular and meaningful marking. If it’s not there then they will probably already be penciling in the “requires improvement” column. With no-notice inspections now in... Continue Reading →
https://www.youtube.com/watch?v=t8XMeocLflc This classic clip "proves" how 25/5 = 14, and does it three different ways. Maths is a powerful method for providing proof - but we need to be careful that each step is based on correct assumptions. One of the most well known fake proofs is as follows: let a = b Then a2... Continue Reading →
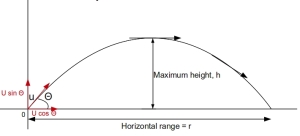
War Maths - Projectile Motion Despite maths having a reputation for being a somewhat bookish subject, it is also an integral part of the seamier side of human nature and has been used by armies to give their side an advantage in wars throughout the ages. Military officers all need to have a firm grasp... Continue Reading →
http://www.youtube.com/watch?v=VIVIegSt81k Hexaflexagons - Amazing Shapes Investigation: Hexaflexagons look at first glance to be somewhat prosaic origami shapes - but like mobius strips they hide some surprises. Flexagons are paper shapes that can be folded to reveal hidden faces - and hexaflexagons themselves have six sides. What's remarkable about hexaflexagons is that during folding, some faces... Continue Reading →
Cracking RSA Code - The World's Most Important Code? RSA code is the basis of all important data transfer. Encrypted data that needs to be sent between two parties, such as banking data or secure communications relies on the techniques of RSA code. RSA code was invented in 1978 by three mathematicians (Rivest, Shamir and... Continue Reading →
http://www.youtube.com/watch?v=G-lN8vWm3m0 The Gorilla in the Room and Other Great Maths Investigations These topics are a great way to add interest to statistics and probability lessons at KS3 and KS4 level, and also a good example of investigations that IB students can conduct. They also have a nice link to ToK - how can we believe... Continue Reading →
Are You Living in a Computer Simulation? This idea might be familiar to fans of The Matrix - and at first glance may seem somewhat unbelievable. However, Oxford University Professor Nick Bostrom makes an interesting case using both conditional probability and logic as to why it's more likely than you might think. The summary of... Continue Reading →
Black Swans and Civilisation Collapse A really interesting branch of mathematics is involved in making future predictions about how civilisation will evolve in the future - and indeed looking at how robust our civilisation is to external shocks. This is one area in which mathematical models do not have a good record as it is... Continue Reading →
How Are Prime Numbers Distributed? Twin Primes Conjecture Thanks to a great post on the Teaching Mathematics blog about getting students to conduct an open ended investigation on consecutive numbers, I tried this with my year 10s - with some really interesting results. My favourites were these conjectures: 1) In a set of any 10... Continue Reading →
Synesthesia - Do Your Numbers Have Colour? Synesthesia is another topic which provides insights into how people perceive numbers - and how a synesthetic's perception of the mathematical world is distinctly different to everyone else's. Those with synesthesia have a cross-wiring of brain activity between 2 of their senses - so for example they may... Continue Reading →
Imagining the 4th Dimension Imagining extra dimensions is a fantastic ToK topic - it is something which seems counter-intuitively false, something which we have no empirical evidence to support, and yet it is something which seems to fit the latest mathematical models on string theory (which requires 11 dimensions). Mathematical models have consistently been shown... Continue Reading →
e's are good - He's Leonard Euler. Having recently starting a topic on the exponential function, I was really struggling to find some good resources online - which is pretty surprising given that e is one of the most important and useful numbers in mathematics. So, here are some possible approaches. 1) e memorisation challenge. This... Continue Reading →
A Maths Snooker Puzzle This was suggested by Paul our Physics teacher - and is a nice little maths puzzle. The maximum break score in snooker is 147 which is achieved by: 15 reds (1 point each) , 15 blacks (7 points each), then yellow ( 2 points), then green (3 points), brown (4 points), blue... Continue Reading →
Maths Invented or Discovered? The PBS Ideas Channel has just released a new video which discusses whether maths is invented by humans, or whether it is discovered (ie whether it can be said to really exist). It's an excellent 10 minute introduction to a pretty complicated topic - and certainly accessible for students: http://www.youtube.com/watch?v=TbNymweHW4E For... Continue Reading →
Which Times Tables do Students Find Difficult? There's an excellent article on today's Guardian Datablog looking at a computer based study (with 232 primary school students) on which times tables students find easiest and difficult. Edited highlights (Guardian quotes in italics): Which multiplication did students get wrong most often? The hardest multiplication was six times... Continue Reading →
Wau: The Most Amazing Number in the World? This is a fantastic video from Vi Hart of Khan Academy. Watch it first and marvel at the properties of this amazing number: https://www.youtube.com/watch?feature=player_embedded&v=GFLkou8NvJo Once you have watched it, watch it again - this time thinking about what number Wau might be - and why you have... Continue Reading →
Cracking ISBN and Credit Card Codes ISBN codes are used on all books published worldwide. It’s a very powerful and useful code, because it has been designed so that if you enter the wrong ISBN code the computer will immediately know – so that you don’t end up with the wrong book. There is lots... Continue Reading →
http://www.youtube.com/watch?v=vIsDjbhbADY Benford's Law - Using Maths to Catch Fraudsters Benford's Law is a very powerful and counter-intuitive mathematical rule which determines the distribution of leading digits (ie the first digit in any number). You would probably expect that distribution would be equal - that a number 9 occurs as often as a number 1. But... Continue Reading →
Simulations -Traffic Jams and Asteroid Impacts You can study the mathematics behind traffic flow using this simulator. Why do traffic jams form? How does the speed limit or traffic lights or the number of lorries on the road affect road conditions? You can run a number of different simulations - looking at ring road traffic,... Continue Reading →
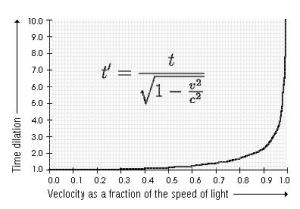
Time Travel and the Speed of Light This is one of my favourite videos from the legendary Carl Sagan. He explains the consequences of near to speed of light travel. https://www.youtube.com/watch?v=lPoGVP-wZv8 This topic fits quite well into a number of mathematical topics - from graphing, to real life uses of equations, to standard form and... Continue Reading →
Even Pigeons Can Do Maths This is a really interesting study from a couple of years ago, which shows that even pigeons can deal with numbers as abstract quantities - in the study the pigeons counted groups of objects in their head and then classified the groups in terms of size. From the New York... Continue Reading →
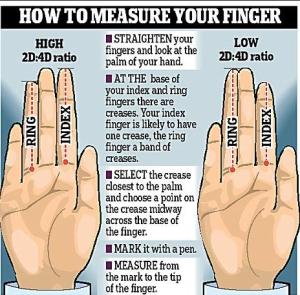
Finger Ratio Predicts Maths Ability? Some of the studies on the 2D: 4D finger ratios (as measured in the picture above) are interesting when considering what factors possibly affect mathematical ability. A 2007 study by Mark Brosnan from the University of Bath found that: "Boys with the longest ring fingers relative to their index fingers... Continue Reading →
Amanda Knox and Bad Maths in Courts This post is inspired by the recent BBC News article, "Amanda Knox and Bad Maths in Courts." The article highlights the importance of good mathematical understanding when handling probabilities - and how mistakes by judges and juries can sometimes lead to miscarriages of justice. A scenario to give to... Continue Reading →