IB Maths Resources from Intermathematics
IB Maths Resources: 300 IB Maths Exploration ideas, video tutorials and Exploration Guides
Teachers can also find 3000 pages of pdf content for IB Maths at my new site: http://www.intermathematics.com. This includes hundreds of worksheets with full worked solutions, treasures hunts, tests and more. I've tried to build connections with real life maths, Theory of Knowledge (ToK) and ideas for maths careers. There are also maths videos, puzzles and... Continue Reading →
One of the main benefits of flipping the classroom is allowing IB maths students to self-teach IB content. There are currently a good number of videos on youtube which allow students to self teach syllabus content, but no real opportunity to watch videos going through IB Higher Level past paper questions. So, I've started to... Continue Reading →
The Telephone Numbers - Graph Theory The telephone numbers are the following sequence: 1, 1, 2, 4, 10, 26, 76, 232, 764, 2620, 9496... (where we start from n=0). This pattern describes the total number of ways which a telephone exchange with n telephones can place a connection between pairs of people. To illustrate this... Continue Reading →
Circular inversions II There are some other interesting properties of circular inversions. One of which is that they preserve the "angle" between intersecting circles. Firstly, how can circles have an angle between them? Well, we draw 2 tangents to both the circles at the point of intersection, and then measure the angle between the 2... Continue Reading →
If you are a teacher then please also visit my new site: intermathematics.com for over 2000+ pdf pages of resources for teaching IB maths! Modelling Infectious Diseases Using mathematics to model the spread of diseases is an incredibly important part of preparing for potential new outbreaks. As well as providing information to health workers about the levels... Continue Reading →
Circular Inversion - Reflecting in a Circle This topic is a great introduction to the idea of mapping - where one point is mapped to another. This is a really useful geometrical tool as it allows complex shapes to be transformed into isomorphic (equivalent) shapes which can sometimes be easier to understand and work with... Continue Reading →
Graphically Understanding Complex Roots If you have studied complex numbers then you'll be familiar with the idea that many polynomials have complex roots. For example x2 + 1 = 0 has the solution x = i and -i. We know that the solution to x2 - 1 = 0 ( x = 1 and -1)... Continue Reading →
This is the British International School Phuket's IB maths exploration page. This list is primarily for IB Maths Applications SL students (exam in 2021 onwards). If you are doing IB Maths Analysis (exam in 2021 onwards) then go to this page instead. Scroll down for the full list of possible topics and ideas! Essential resources for IB students:... Continue Reading →
This post is based on the fantastic PlusMaths article on bluffing- which is a great introduction to this topic. If you're interested then it's well worth a read. This topic shows the power of mathematics in solving real world problems - and combines a wide variety of ideas and methods - probability, Game Theory, calculus,... Continue Reading →
The Riemann Sphere The Riemann Sphere is a fantastic glimpse of where geometry can take you when you escape from the constraints of Euclidean Geometry - the geometry of circles and lines taught at school. Riemann, the German 19th Century mathematician, devised a way of representing every point on a plane as a point on... Continue Reading →
Divisibility tests allow us to calculate whether a number can be divided by another number. For example, can 354 be divided by 3? Can 247,742 be divided by 11? So what are the rules behind divisibility tests, and more interestingly, how can we prove them? Divisibility rule for 3 The most well known divisibility rule... Continue Reading →
The Goldbach Conjecture is one of the most famous problems in mathematics. It has remained unsolved for over 250 years - after being proposed by German mathematician Christian Goldbach in 1742. Anyone who could provide a proof would certainly go down in history as one of the true great mathematicians. The conjecture itself is deceptively... Continue Reading →
http://www.youtube.com/watch?v=K8SkCh-n4rw The Gambler's Fallacy The above video is an excellent introduction to the gambler's fallacy. This is the misconception that prior outcomes will have an effect on subsequent independent events. The classic example for this is the gambler who watches a run of 9 blacks on a roulette wheel with only red and black, and... Continue Reading →
Cracking RSA Code - The World's Most Important Code? RSA code is the basis of all important data transfer. Encrypted data that needs to be sent between two parties, such as banking data or secure communications relies on the techniques of RSA code. RSA code was invented in 1978 by three mathematicians (Rivest, Shamir and... Continue Reading →
Maths IA – 300 Maths Exploration Topics: Scroll down this page to find over 300 examples of maths IA exploration topics and ideas for IB mathematics students doing their internal assessment (IA) coursework. Topics include Algebra and Number (proof), Geometry, Calculus, Statistics and Probability, Physics, and links with other subjects. Suitable for Applications and Interpretations... Continue Reading →
http://www.youtube.com/watch?v=G-lN8vWm3m0 The Gorilla in the Room and Other Great Maths Investigations These topics are a great way to add interest to statistics and probability lessons at KS3 and KS4 level, and also a good example of investigations that IB students can conduct. They also have a nice link to ToK - how can we believe... Continue Reading →
Are You Living in a Computer Simulation? This idea might be familiar to fans of The Matrix - and at first glance may seem somewhat unbelievable. However, Oxford University Professor Nick Bostrom makes an interesting case using both conditional probability and logic as to why it's more likely than you might think. The summary of... Continue Reading →
Bridge Building Lesson Plan Learning Objectives: Students are introduced to one of the many careers that they can pursue through mathematics. 5 minutes: Brainstorm – why is mathematics useful for engineering? What kinds of jobs do engineers do? (refer to maths careers site – a large number of well paid jobs are in engineering) 5... Continue Reading →
Black Swans and Civilisation Collapse A really interesting branch of mathematics is involved in making future predictions about how civilisation will evolve in the future - and indeed looking at how robust our civilisation is to external shocks. This is one area in which mathematical models do not have a good record as it is... Continue Reading →
The Riemann Hypothesis Explained This is quite a complex topic probably only accessible for high achieving HL IB students, but nevertheless it's still a fascinating introduction to one of the most important (and valuable) unsolved problems in pure mathematics. Firstly, the Riemann Hypothesis is concerned with the Riemann zeta function. This function is defined in... Continue Reading →
How Are Prime Numbers Distributed? Twin Primes Conjecture Thanks to a great post on the Teaching Mathematics blog about getting students to conduct an open ended investigation on consecutive numbers, I tried this with my year 10s - with some really interesting results. My favourites were these conjectures: 1) In a set of any 10... Continue Reading →
Synesthesia - Do Your Numbers Have Colour? Synesthesia is another topic which provides insights into how people perceive numbers - and how a synesthetic's perception of the mathematical world is distinctly different to everyone else's. Those with synesthesia have a cross-wiring of brain activity between 2 of their senses - so for example they may... Continue Reading →
Imagining the 4th Dimension Imagining extra dimensions is a fantastic ToK topic - it is something which seems counter-intuitively false, something which we have no empirical evidence to support, and yet it is something which seems to fit the latest mathematical models on string theory (which requires 11 dimensions). Mathematical models have consistently been shown... Continue Reading →
e's are good - He's Leonard Euler. Having recently starting a topic on the exponential function, I was really struggling to find some good resources online - which is pretty surprising given that e is one of the most important and useful numbers in mathematics. So, here are some possible approaches. 1) e memorisation challenge. This... Continue Reading →
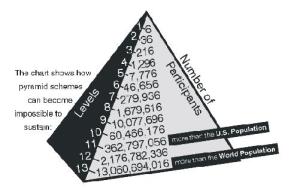
The Mathematics of Cons - Pyramid Selling Pyramid schemes are a very old con - but whilst illegal, still exist in various forms. Understanding the maths behind them therefore is a good way to avoid losing your savings! The most basic version of the fraud starts with an individual making the following proposition, "pay me... Continue Reading →
A Maths Snooker Puzzle This was suggested by Paul our Physics teacher - and is a nice little maths puzzle. The maximum break score in snooker is 147 which is achieved by: 15 reds (1 point each) , 15 blacks (7 points each), then yellow ( 2 points), then green (3 points), brown (4 points), blue... Continue Reading →
Maths Invented or Discovered? The PBS Ideas Channel has just released a new video which discusses whether maths is invented by humans, or whether it is discovered (ie whether it can be said to really exist). It's an excellent 10 minute introduction to a pretty complicated topic - and certainly accessible for students: http://www.youtube.com/watch?v=TbNymweHW4E For... Continue Reading →
Which Times Tables do Students Find Difficult? There's an excellent article on today's Guardian Datablog looking at a computer based study (with 232 primary school students) on which times tables students find easiest and difficult. Edited highlights (Guardian quotes in italics): Which multiplication did students get wrong most often? The hardest multiplication was six times... Continue Reading →
Wau: The Most Amazing Number in the World? This is a fantastic video from Vi Hart of Khan Academy. Watch it first and marvel at the properties of this amazing number: https://www.youtube.com/watch?feature=player_embedded&v=GFLkou8NvJo Once you have watched it, watch it again - this time thinking about what number Wau might be - and why you have... Continue Reading →
Cracking ISBN and Credit Card Codes ISBN codes are used on all books published worldwide. It’s a very powerful and useful code, because it has been designed so that if you enter the wrong ISBN code the computer will immediately know – so that you don’t end up with the wrong book. There is lots... Continue Reading →
NASA, Aliens and Binary Codes from the Star The Drake Equation was intended by astronomer Frank Drake to spark a dialogue about the odds of intelligent life on other planets. He was one of the founding members of SETI - the Search for Extra Terrestrial Intelligence - which has spent the past 50 years scanning... Continue Reading →
http://www.youtube.com/watch?v=vIsDjbhbADY Benford's Law - Using Maths to Catch Fraudsters Benford's Law is a very powerful and counter-intuitive mathematical rule which determines the distribution of leading digits (ie the first digit in any number). You would probably expect that distribution would be equal - that a number 9 occurs as often as a number 1. But... Continue Reading →
Simulations -Traffic Jams and Asteroid Impacts You can study the mathematics behind traffic flow using this simulator. Why do traffic jams form? How does the speed limit or traffic lights or the number of lorries on the road affect road conditions? You can run a number of different simulations - looking at ring road traffic,... Continue Reading →
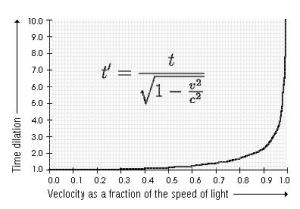
Time Travel and the Speed of Light This is one of my favourite videos from the legendary Carl Sagan. He explains the consequences of near to speed of light travel. https://www.youtube.com/watch?v=lPoGVP-wZv8 This topic fits quite well into a number of mathematical topics - from graphing, to real life uses of equations, to standard form and... Continue Reading →
Even Pigeons Can Do Maths This is a really interesting study from a couple of years ago, which shows that even pigeons can deal with numbers as abstract quantities - in the study the pigeons counted groups of objects in their head and then classified the groups in terms of size. From the New York... Continue Reading →
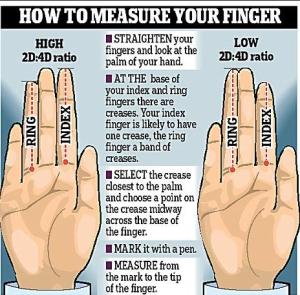
Finger Ratio Predicts Maths Ability? Some of the studies on the 2D: 4D finger ratios (as measured in the picture above) are interesting when considering what factors possibly affect mathematical ability. A 2007 study by Mark Brosnan from the University of Bath found that: "Boys with the longest ring fingers relative to their index fingers... Continue Reading →
Amanda Knox and Bad Maths in Courts This post is inspired by the recent BBC News article, "Amanda Knox and Bad Maths in Courts." The article highlights the importance of good mathematical understanding when handling probabilities - and how mistakes by judges and juries can sometimes lead to miscarriages of justice. A scenario to give to... Continue Reading →
Does it Pay to be Nice? Game Theory and Evolution Game theory is an interesting branch of mathematics with links across a large number of disciplines - from politics to economics to biology and psychology. The most well known example is that of the Prisoner's Dilemma. (Illustrated below). Two prisoners are taken into custody and... Continue Reading →
Is God a Mathematician? http://www.youtube.com/watch?v=jremlZvNDuk&feature=youtu.be That's the provocative question posed by American Physicist Michio Kaku in this fascinating 5 minute interview which takes in the ideas of Newton, Einstein and modern ideas on String Theory. It addresses the fundamental questions in maths ToK - is mathematics invented or discovered? What explains the "unreasonable effectiveness" of... Continue Reading →
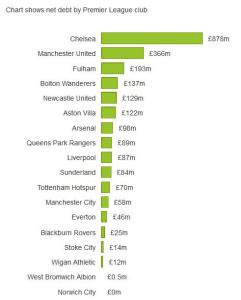
Premier League Finances - Debt and Wages This is a great article from the Guardian DataBlog analysing the finances for last season's Premier League clubs. As the Guardian says, "More than two thirds of the Premier League's record £2.4bn income in 2011-12 was paid out in wages, according to the most recently published accounts of... Continue Reading →
This is inspired by a fantastic website - we use math - which has a massive amount of information about different careers using mathematics in a really well laid out format. According to a comprehensive careers survey by Careers Cast - which looked at over 200 different jobs and ranked them for stress, pay, job... Continue Reading →
Michio Kaku - American Professor of Theoretical Physics and fantastic populariser of mathematics and physics takes us through a 40 minute journey on the importance of physics in explaining the universe: http://www.youtube.com/watch?v=0NbBjNiw4tk Great stuff - well worth watching!
Graham's Number - literally big enough to collapse your head into a black hole Graham's Number is a number so big that it would literally collapse your head into a black hole were you fully able to comprehend it. And that's not hyperbole - the informational content of Graham's Number is so astronomically large that... Continue Reading →
Plus Maths has a large number of great podcasts which look at maths ToK topics: 1) An interview with Max Tegmark (pictured above) about why he thinks that the universe is itself a mathematical structure. 2) An interview with physicists David Berman about how many dimensions exist. 3) A talk with cosmologist John Barrow about... Continue Reading →
http://www.youtube.com/watch?v=PCu_BNNI5x4 What is the sum of the infinite sequence 1, -1, 1, -1, 1.....? This is a really interesting puzzle to study - which fits very well when studying geometric series, proof and the history of maths. The two most intuitive answers are either that it has no sum or that it sums to zero. ... Continue Reading →
There are a lot of good general sequence puzzles on the website Fibonicci. For example find the next term of: 1) 15, 29, 56, 108, 208 2) 13, -21, 34, -55, 89 3) 52, 56, 48, 64, 32 4) 230, 460, 46, 92, 9.2 5) 68, 36, 20, 12, 8 Answers (in white text -... Continue Reading →
There are some great telescope pictures of the universe on the Guardian Science Gallery this month. This picture shows the distorted remnants of a supernova explosion - where stars are destroyed. This particular supernova is 26,000 light years from Earth - meaning that this is a picture 26,000 years into the past. It is thought... Continue Reading →
This is another interesting maths sequence puzzle: When x = 1, y = 1, when x= 2, y = -1, when x = 3, y = 1, a) if when x = 4, y = -1, what formula gives the nth term? b) if when x = 4, y = 3, what formula gives the... Continue Reading →
This is a huge topic - closely related to some of the Theory of knowledge concepts. It also gets very complicated. Here are some of the basics (some of this information is simplified from the Stanford Encyclopedia which goes into far more detail). 1) Platonism The basic philosophical question in maths is ontological - ie concerned with... Continue Reading →
This is the first post to just link to a TES contributor rather than a specific resource, but SRWhitehouse has provided a massive number of high quality worksheets on IB (and A level) topics - there's a huge number of worksheets to choose from, everything from trig graphs to proof by induction to logs to... Continue Reading →