IB Maths Resources: 300 IB Maths Exploration ideas, video tutorials and Exploration Guides
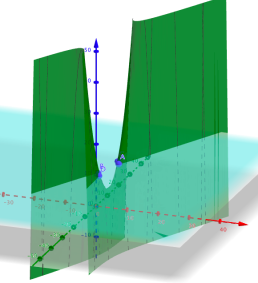
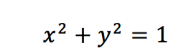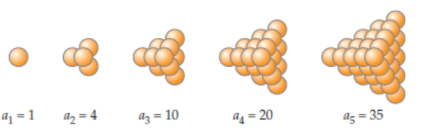Generating e through probability and hypercubes This is a really beautiful solution to an interesting probability problem posed by fellow IB teacher Daniel Hwang, for which I've outlined a method for solving suggested by Ferenc Beleznay. The problem is as follows: On average, how many random real numbers from 0 to 1 (inclusive) are required... Continue Reading →
Have you got a Super Brain? Adapting and exploring maths challenge problems is an excellent way of finding ideas for IB maths explorations and extended essays. This problem is taken from the book: The first 25 years of the Superbrain challenges. I'm going to see how many different ways I can solve it. The problem... Continue Reading →
Paper 3 investigations Introduction Below are a selection of the Paper 3 investigations I've made over the years. Many of these bridge between Paper 3 practice (exposure to novel or new mathematical ideas) and the Exploration coursework. All of these could be easily adapted to make some very interesting coursework submissions. If you are a... Continue Reading →
3D Printing with Desmos: Stewie Griffin Using Desmos or Geogebra to design a picture or pattern is quite a nice exploration topic - but here's an idea to make your investigation stand out from the crowd - how about converting your image to a 3D printed design? Step 1 Create an image on Desmos or... Continue Reading →
Complex Numbers as Matrices - Euler's Identity Euler's Identity below is regarded as one of the most beautiful equations in mathematics as it combines five of the most important constants in mathematics: I'm going to explore whether we can still see this relationship hold when we represent complex numbers as matrices. Complex Numbers as Matrices... Continue Reading →
Sierpinski Triangle: A picture of infinity This pattern of a Sierpinski triangle pictured above was generated by a simple iterative program. I made it by modifying the code previously used to plot the Barnsley Fern. You can run the code I used on repl.it. What we are seeing is the result of 30,000 iterations of a simple... Continue Reading →
Sphere packing problem: Pyramid design Sphere packing problems are a maths problems which have been considered over many centuries - they concern the optimal way of packing spheres so that the wasted space is minimised. You can achieve an average packing density of around 74% when you stack many spheres together, but today I want to... Continue Reading →
Martingale II and Currency Trading We can use computer coding to explore game strategies and also to help understand the underlying probability distribution functions. Let's start with a simple game where we toss a coin 4 times, stake 1 counter each toss and always call heads. This would give us a binomial distribution with... Continue Reading →
Time dependent gravity and cosmology! In our universe we have a gravitational constant - i.e gravity is not dependent on time. If gravity changed with respect to time then the gravitational force exerted by the Sun on Earth would lessen (or increase) over time with all other factors remaining the same. Interestingly time-dependent gravity was... Continue Reading →
https://giphy.com/gifs/KAe4nRWH6PlwGqnJJZ The Tusi couple - A circle rolling inside a circle Numberphile have done a nice video where they discuss some beautiful examples of trigonometry and circular motion and where they present the result shown above: a circle rolling within a circle, with the individual points on the small circle showing linear motion along the... Continue Reading →
IB Maths Exploration Guides Below you can download some comprehensive exploration guides that I've written to help students get excellent marks on their IB maths coursework. These guides are suitable for both Analysis and also Applications students. Over the past several years I've written over 200 posts with exploration ideas and marked hundreds of IAs... Continue Reading →
https://www.youtube.com/watch?v=Ry3B9hJbBfk The Martingale system The Martingale system was first used in France in 1700s gambling halls and remains used today in some trading strategies. I'll look at some of the mathematical ideas behind this and why it has remained popular over several centuries despite having a long term expected return of zero. The scenario You... Continue Reading →
Projectiles IV: Time dependent gravity! This carries on our exploration of projectile motion - this time we will explore what happens if gravity is not fixed, but is instead a function of time. (This idea was suggested by and worked through by fellow IB teachers Daniel Hwang and Ferenc Beleznay). In our universe we... Continue Reading →
Projectile Motion III: Varying gravity We can also do some interesting things with projectile motion if we vary the gravitational pull when we look at projectile motion. The following graphs are all plotted in parametric form. Here t is the parameter, v is the initial velocity which we will keep constant, theta is the angle... Continue Reading →
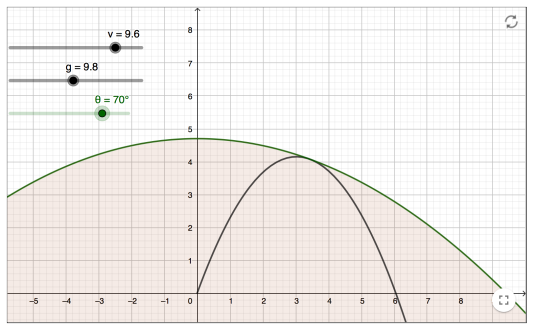
Projectile Motion Investigation II Another example for investigating projectile motion has been provided by fellow IB teacher Ferenc Beleznay. Here we fix the velocity and then vary the angle, then to plot the maximum points of the parabolas. He has created a Geogebra app to show this (shown above). The locus of these maximum points... Continue Reading →
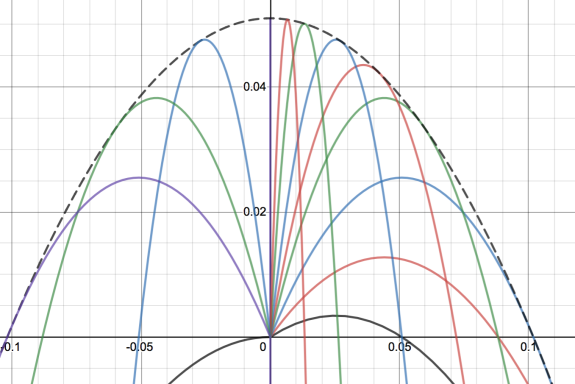
Envelope of projectile motion For any given launch angle and for a fixed initial velocity we will get projectile motion. In the graph above I have changed the launch angle to generate different quadratics. The black dotted line is then called the envelope of all these lines, and is the boundary line formed when I... Continue Reading →
https://www.youtube.com/watch?v=1EkoaQJyrfk Classical Geometry Puzzle: Finding the Radius This is another look at a puzzle from Mind Your Decisions. The problem is to find the radius of the following circle: We are told that line AD and BC are perpendicular and the lengths of some parts of chords, but not much more! First I'll look at... Continue Reading →
Further investigation of the Mordell Equation This post carries on from the previous post on the Mordell Equation - so make sure you read that one first - otherwise this may not make much sense. The man pictured above (cite: Wikipedia) is Louis Mordell who studied the equations we are looking at today (and which... Continue Reading →
The Mordell Equation [Fermat's proof] Let's have a look at a special case of the Mordell Equation, which looks at the difference between an integer cube and an integer square. In this case we want to find all the integers x,y such that the difference between the cube and the square gives 2. These sorts... Continue Reading →
https://www.youtube.com/watch?v=RI2p-e7dL3E Can you solve Oxford University's Interview Question? The excellent Youtube channel Mind Your Decisions is a gold mine for potential IB maths exploration topics. I'm going to follow through my own approach to problem posed in the video. The problem is to be able to trace the movement of the midpoint of a ladder... Continue Reading →
Using Maths to model the spread of Coronavirus (COVID-19) This coronavirus is the latest virus to warrant global fears over a disease pandemic. Throughout history we have seen pandemic diseases such as the Black Death in Middle Ages Europe and the Spanish Flu at the beginning of the 20th century. More recently we have seen... Continue Reading →
Square Triangular Numbers Square triangular numbers are numbers which are both square numbers and also triangular numbers - i.e they can be arranged in a square or a triangle. The picture above (source: wikipedia) shows that 36 is both a square number and also a triangular number. The question is how many other square triangular... Continue Reading →
https://www.youtube.com/watch?v=ZOiF7ZlboXA Rational Approximations to Irrational Numbers This year two mathematicians (James Maynard and Dimitris Koukoulopoulos) managed to prove a long-standing Number Theory problem called the Duffin Schaeffer Conjecture. The problem is concerned with the ability to obtain rational approximations to irrational numbers. For example, a rational approximation to pi is 22/7. This gives 3.142857 and... Continue Reading →
When do 2 squares equal 2 cubes? Following on from the hollow square investigation this time I will investigate what numbers can be written as both the sum of 2 squares, 2 cubes and 2 powers of 4. i.e a2+b2 = c3+d3 = e4+f4. Geometrically we can think of this as trying to find an... Continue Reading →
Hollow Cubes investigation Hollow cubes like the picture above [reference] are an extension of the hollow squares investigation done previously. This time we can imagine a 3 dimensional stack of soldiers, and so try to work out which numbers of soldiers can be arranged into hollow cubes. Therefore what we need to find is what... Continue Reading →
Ramanujan's Taxi Cabs and the Sum of 2 Cubes The Indian mathematician Ramanujan (picture cite: Wikipedia) is renowned as one of great self-taught mathematical prodigies. His correspondence with the renowned mathematician G. H Hardy led him to being invited to study in England, though whilst there he fell sick. Visiting him in hospital, Hardy remarked that... Continue Reading →
Waging war with maths: Hollow squares The picture above [US National Archives, Wikipedia] shows an example of the hollow square infantry formation which was used in wars over several hundred years. The idea was to have an outer square of men, with an inner empty square. This then allowed the men in the formation to... Continue Reading →
Finding the volume of a rugby ball (prolate spheroid) With the rugby union World Cup currently underway I thought I'd try and work out the volume of a rugby ball using some calculus. This method works similarly for American football and Australian rules football. The approach is to consider the rugby ball as an... Continue Reading →
The Shoelace Algorithm to find areas of polygons This is a nice algorithm, formally known as Gauss's Area formula, which allows you to work out the area of any polygon as long as you know the Cartesian coordinates of the vertices. The case can be shown to work for all triangles, and then can be... Continue Reading →
Soap Bubbles and Catenoids Soap bubbles form such that they create a shape with the minimum surface area for the given constraints. For a fixed volume the minimum surface area is a sphere, which is why soap bubbles will form spheres where possible. We can also investigate what happens when a soap film is formed... Continue Reading →
For students taking their exams in 2021 there is a big change to the IB syllabus - there will now be 4 possible strands: IB HL Analysis and Approaches, IB SL Analysis and Approaches, IB HL Applications and Interpretations, IB SL Applications and Interpretations. IB Applications and Interpretations There is a reasonable cross-over between the... Continue Reading →
Teacher resources I have collected together below a lot of (hopefully!) useful resources to support IB teachers teaching IB Maths Analysis SL and HL and also Applications SL and HL. This is a small portion of the content on my new site: intermathematics.com which has been designed specifically for teachers of mathematics at international schools. ... Continue Reading →
https://www.youtube.com/watch?v=Zs2M7gWSbTg Simulating a Football Season This is a nice example of how statistics are used in modeling - similar techniques are used when gambling companies are creating odds or when computer game designers are making football manager games. We start with some statistics. The soccer stats site has the data we need from the 2018-19... Continue Reading →
https://www.youtube.com/watch?v=etMJxB-igrc The Van Eck Sequence This is a nice sequence as discussed in the Numberphile video above. There are only 2 rules: If you have not seen the number in the sequence before, add a 0 to the sequence. If you have seen the number in the sequence before, count how long since you... Continue Reading →
Computers can brute force a lot of simple mathematical problems, so I thought I'd try and write some code to solve some of them. In nearly all these cases there's probably a more elegant way of coding the problem - but these all do the job! You can run all of these with a Python... Continue Reading →
https://www.youtube.com/watch?v=q6L06pyt9CA Stacking cannonballs - solving maths with code Numberphile have recently done a video looking at the maths behind stacking cannonballs - so in this post I'll look at the code needed to solve this problem. Triangular based pyramid. A triangular based pyramid would have: 1 ball on the top layer 1 + 3 balls... Continue Reading →
https://www.youtube.com/watch?v=FFftmWSzgmk Plotting the Mandelbrot Set The video above gives a fantastic account of how we can use technology to generate the Mandelbrot Set - one of the most impressive mathematical structures you can imagine. The Mandelbrot Set can be thought of as an infinitely large picture - which contains fractal patterns no matter how far... Continue Reading →
https://www.youtube.com/watch?v=Wim9WJeDTHQ What's so special about 277777788888899? Numberphile have just done a nice video which combines mathematics and computer programing. The challenge is to choose any number (say 347) Then we do 3x4x7 = 84 next we do 8x4 = 32 next we do 3x2 = 6. And when we get to a single digit number... Continue Reading →
https://www.youtube.com/watch?v=5TkIe60y2GI Normal Numbers - and random number generators Numberphile have a nice new video where Matt Parker discusses all different types of numbers - including "normal numbers". Normal numbers are defined as irrational numbers for which the probability of choosing any given 1 digit number is the same, the probability of choosing any given 2... Continue Reading →
Crack the Beale Papers and find a $65 Million buried treasure? The story of a priceless buried treasure of gold, silver and jewels (worth around $65 million in today's money) began in January 1822. A stranger by the name of Thomas Beale walked into the Washington Hotel Virginia with a locked iron box, which he gave... Continue Reading →
Volume optimization of a cuboid This is an extension of the Nrich task which is currently live - where students have to find the maximum volume of a cuboid formed by cutting squares of size x from each corner of a 20 x 20 piece of paper. I'm going to use an n x 10 rectangle... Continue Reading →
Projective Geometry Geometry is a discipline which has long been subject to mathematical fashions of the ages. In classical Greece, Euclid’s elements (Euclid pictured above) with their logical axiomatic base established the subject as the pinnacle on the “great mountain of Truth” that all other disciplines could but hope to scale. However the status of... Continue Reading →
https://www.youtube.com/watch?v=4aMtJ-V26Z4 Narcissistic Numbers Narcissistic Numbers are defined as follows: An n digit number is narcissistic if the sum of its digits to the nth power equal the original number. For example with 2 digits, say I choose the number 36: 32 + 62 = 45. Therefore 36 is not a narcissistic number, as my answer... Continue Reading →
https://www.youtube.com/watch?v=fcfQkxwz4Oo Quantum Mechanics - Statistical Universe Quantum mechanics is the name for the mathematics that can describe physical systems on extremely small scales. When we deal with the macroscopic - i.e scales that we experience in our everyday physical world, then Newtonian mechanics works just fine. However on the microscopic level of particles, Newtonian mechanics... Continue Reading →
Modeling hours of daylight Desmos has a nice student activity (on teacher.desmos.com) modeling the number of hours of daylight in Florida versus Alaska - which both produce a nice sine curve when plotted on a graph. So let's see if this relationship also holds between Phuket and Manchester. First we can find the daylight hours... Continue Reading →
Cartoon from here The Gini Coefficient - Measuring Inequality The Gini coefficient is a value ranging from 0 to 1 which measures inequality. 0 represents perfect equality - i.e everyone in a population has exactly the same wealth. 1 represents complete inequality - i.e 1 person has all the wealth and everyone else has nothing.... Continue Reading →
Is Intergalactic space travel possible? The Andromeda Galaxy is around 2.5 million light years away - a distance so large that even with the speed of light at traveling as 300,000,000m/s it has taken 2.5 million years for that light to arrive. The question is, would it ever be possible for a journey to the... Continue Reading →
This is a nice example of using some maths to solve a puzzle from the mindyourdecisions youtube channel (screencaptures from the video). How to Avoid The Troll: A Puzzle In these situations it's best to look at the extreme case first so you get some idea of the problem. If you are feeling particularly pessimistic... Continue Reading →
http://www.youtube.com/watch?v=skM37PcZmWE Zeno's Paradox - Achilles and the Tortoise This is a very famous paradox from the Greek philosopher Zeno - who argued that a runner (Achilles) who constantly halved the distance between himself and a tortoise would never actually catch the tortoise. The video above explains the concept. There are two slightly different versions to... Continue Reading →
Fourier Transform The Fourier Transform and the associated Fourier series is one of the most important mathematical tools in physics. Physicist Lord Kelvin remarked in 1867: "Fourier's theorem is not only one of the most beautiful results of modern analysis, but it may be said to furnish an indispensable instrument in the treatment of nearly... Continue Reading →