Classical Geometry Puzzle: Finding the Radius
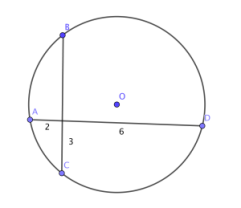
This is another look at a puzzle from Mind Your Decisions. The problem is to find the radius of the following circle:
We are told that line AD and BC are perpendicular and the lengths of some parts of chords, but not much more! First I’ll look at my attempt to solve this. It’s not quite as “nice” as the solution in the video as it requires the use of a calculator, but it still does the job.
Method 1, extra construction lines:
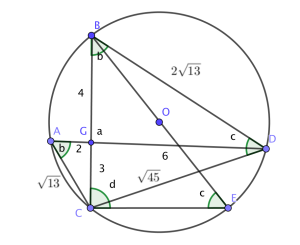
These are the extra construction lines required to solve this problem. Here is the step by step thought process:
- Find the hypotenuse of triangle AGC.
- Use the circle theorem angles in the same segment are equal to show that angle CBD = angle CAG.
- Therefore triangle AGC and GBD are similar, so length BG = 4. We can now use Pythagoras to find length BD.
- We can find length CD by Pythagoras.
- Now we have 3 sides of a triangle, CDB. This allows use to find angle BDC using the cosine rule.
- Now we the circle theorem angles in the same segment are equal to show that angle BDC = angle BEC.
- Now we use the circle theorem angles in a semi circle are 90 degrees to show ECB = 90.
- Now we have a right angled triangle BCE where we know both an angle and a side, so can use trigonometry to find the length of BE.
- Therefore the radius is approximately 4.03.
Method 2, creating a coordinate system
This is a really beautiful solution – which does not require a calculator (and which is discussed in the video above). We start by creating a coordinate system based around point G at (0,0). Because we have perpendicular lines we can therefore create coordinates for A, B and C. We also mark the centre of the circle as (p,q).
First we start with the equation of a circle centre (p.q):
Next we create 3 equations by substituting in our coordinates:
Next we can do equation (3) – equation (1) to give:
Next we can substitute this value for p into equations (1) and (3) and equate to get:
Lastly we can substitute both values for p and q into equation (1) to find r:
We get the same answer as before – though this definitely feels like a “cleaner” solution. There are other ways to solve this – but some of these require the use of equations you may not already know (such as the law of sines in a circumcircle, or the equation for perpendicular chords and radius). Perhaps explore any other methods for solving this – what are the relative merits of each approach?
IB teacher? Please visit my new site http://www.intermathematics.com ! Hundreds of IB worksheets, unit tests, mock exams, treasure hunt activities, paper 3 activities, coursework support and more. Take some time to explore!
Are you a current IB student or IB teacher? Do you want to learn the tips and tricks to produce excellent Mathematics coursework? Check out my new IA Course in the menu!

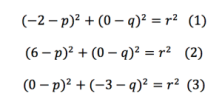

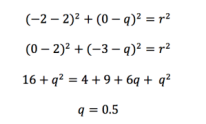

Leave a Reply