IB Maths Resources from Intermathematics
IB Maths Resources: 300 IB Maths Exploration ideas, video tutorials and Exploration Guides
Projective Geometry Geometry is a discipline which has long been subject to mathematical fashions of the ages. In classical Greece, Euclid’s elements (Euclid pictured above) with their logical axiomatic base established the subject as the pinnacle on the “great mountain of Truth” that all other disciplines could but hope to scale. However the status of... Continue Reading →
Hyperbolic Geometry The usual geometry taught in school is that of Euclidean geometry - in which angles in a triangle add up 180 degrees. This is based on the idea that the underlying space on which the triangle is drawn is flat. However, if the underlying space in curved then this will no longer be... Continue Reading →
http://www.youtube.com/watch?v=skM37PcZmWE Zeno's Paradox - Achilles and the Tortoise This is a very famous paradox from the Greek philosopher Zeno - who argued that a runner (Achilles) who constantly halved the distance between himself and a tortoise would never actually catch the tortoise. The video above explains the concept. There are two slightly different versions to... Continue Reading →
Non Euclidean Geometry V - Pseudospheres and other amazing shapes Non Euclidean geometry takes place on a number of weird and wonderful shapes. Remember, one of fundamental questions mathematicians investigating the parallel postulate were asking was how many degrees would a triangle have in that geometry- and it turns out that this question can be... Continue Reading →
This post follows on from Non-Euclidean Geometry – An Introduction – read that one first! Non Euclidean Geometry IV - New Universes The 19th century saw mathematicians finally throw off the shackles of Euclid's 5th (parallel) postulate - and go on to discover a bewildering array of geometries which no longer took this assumption about... Continue Reading →
Non Euclidean Geometry - Spherical Geometry This article follow on from Non Euclidean Geometry - An Introduction - read that first!Most geometers up until the 19th century had focused on trying to prove that Euclid's 5th (parallel) postulate was true. The underlying assumption was that Euclidean geometry was true and therefore the 5th postulate must... Continue Reading →
Non-Euclidean Geometry - A New UniverseThis post follows on from Non-Euclidean Geometry - An Introduction - read that one first! The Hungarian army officer and mathematician Johan Bolyai wrote to his father in 1823 in excitement at his mathematical breakthrough with regards to the parallel postulate. "I have created a new universe from nothing." Johan... Continue Reading →
Non Euclidean Geometry - An Introduction It wouldn't be an exaggeration to describe the development of non-Euclidean geometry in the 19th Century as one of the most profound mathematical achievements of the last 2000 years. Ever since Euclid (c. 330-275BC) included in his geometrical proofs an assumption (postulate) about parallel lines, mathematicians had been trying... Continue Reading →
http://www.youtube.com/watch?v=w-I6XTVZXww Unbelievable: 1+2+3+4.... = -1/12 ? The above video by the excellent team at Numberphile has caused a bit of an internet stir - by providing a proof that 1+2+3+4+5+... = -1/12 It's well worth watching as an example of what proof means - if something is proved which we "know" is wrong, then should... Continue Reading →
Is maths invented or discovered? One of the most interesting questions to investigate with regards to maths Theory of Knowledge (ToK) is the relationship between maths and reality. Why does maths describe reality? Are the mathematical equations of Newton and Einstein inventions to describe reality, or did they exist prior to their discovery? If equations... Continue Reading →
The Riemann Sphere The Riemann Sphere is a fantastic glimpse of where geometry can take you when you escape from the constraints of Euclidean Geometry - the geometry of circles and lines taught at school. Riemann, the German 19th Century mathematician, devised a way of representing every point on a plane as a point on... Continue Reading →
https://www.youtube.com/watch?v=t8XMeocLflc This classic clip "proves" how 25/5 = 14, and does it three different ways. Maths is a powerful method for providing proof - but we need to be careful that each step is based on correct assumptions. One of the most well known fake proofs is as follows: let a = b Then a2... Continue Reading →
Western music has its roots in the harmonics discovered by Pythagoras - himself a keen musician - over 2000 years ago. Pythagoras noticed that certain string ratios would produce sounds that were in harmony with each other. The simplest example is illustrated above with an electric guitar. When a string is played, and then that... Continue Reading →
Maths IA – 300 Maths Exploration Topics: Scroll down this page to find over 300 examples of maths IA exploration topics and ideas for IB mathematics students doing their internal assessment (IA) coursework. Topics include Algebra and Number (proof), Geometry, Calculus, Statistics and Probability, Physics, and links with other subjects. Suitable for Applications and Interpretations... Continue Reading →
http://www.youtube.com/watch?v=G-lN8vWm3m0 The Gorilla in the Room and Other Great Maths Investigations These topics are a great way to add interest to statistics and probability lessons at KS3 and KS4 level, and also a good example of investigations that IB students can conduct. They also have a nice link to ToK - how can we believe... Continue Reading →
Are You Living in a Computer Simulation? This idea might be familiar to fans of The Matrix - and at first glance may seem somewhat unbelievable. However, Oxford University Professor Nick Bostrom makes an interesting case using both conditional probability and logic as to why it's more likely than you might think. The summary of... Continue Reading →
Black Swans and Civilisation Collapse A really interesting branch of mathematics is involved in making future predictions about how civilisation will evolve in the future - and indeed looking at how robust our civilisation is to external shocks. This is one area in which mathematical models do not have a good record as it is... Continue Reading →
The Riemann Hypothesis Explained This is quite a complex topic probably only accessible for high achieving HL IB students, but nevertheless it's still a fascinating introduction to one of the most important (and valuable) unsolved problems in pure mathematics. Firstly, the Riemann Hypothesis is concerned with the Riemann zeta function. This function is defined in... Continue Reading →
Synesthesia - Do Your Numbers Have Colour? Synesthesia is another topic which provides insights into how people perceive numbers - and how a synesthetic's perception of the mathematical world is distinctly different to everyone else's. Those with synesthesia have a cross-wiring of brain activity between 2 of their senses - so for example they may... Continue Reading →
Imagining the 4th Dimension Imagining extra dimensions is a fantastic ToK topic - it is something which seems counter-intuitively false, something which we have no empirical evidence to support, and yet it is something which seems to fit the latest mathematical models on string theory (which requires 11 dimensions). Mathematical models have consistently been shown... Continue Reading →
Maths Invented or Discovered? The PBS Ideas Channel has just released a new video which discusses whether maths is invented by humans, or whether it is discovered (ie whether it can be said to really exist). It's an excellent 10 minute introduction to a pretty complicated topic - and certainly accessible for students: http://www.youtube.com/watch?v=TbNymweHW4E For... Continue Reading →
NASA, Aliens and Binary Codes from the Star The Drake Equation was intended by astronomer Frank Drake to spark a dialogue about the odds of intelligent life on other planets. He was one of the founding members of SETI - the Search for Extra Terrestrial Intelligence - which has spent the past 50 years scanning... Continue Reading →
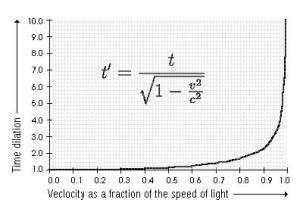
Time Travel and the Speed of Light This is one of my favourite videos from the legendary Carl Sagan. He explains the consequences of near to speed of light travel. https://www.youtube.com/watch?v=lPoGVP-wZv8 This topic fits quite well into a number of mathematical topics - from graphing, to real life uses of equations, to standard form and... Continue Reading →
Even Pigeons Can Do Maths This is a really interesting study from a couple of years ago, which shows that even pigeons can deal with numbers as abstract quantities - in the study the pigeons counted groups of objects in their head and then classified the groups in terms of size. From the New York... Continue Reading →
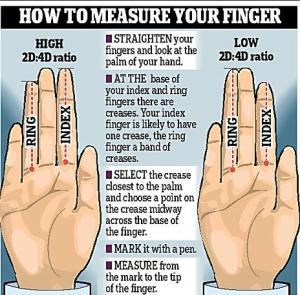
Finger Ratio Predicts Maths Ability? Some of the studies on the 2D: 4D finger ratios (as measured in the picture above) are interesting when considering what factors possibly affect mathematical ability. A 2007 study by Mark Brosnan from the University of Bath found that: "Boys with the longest ring fingers relative to their index fingers... Continue Reading →
Amanda Knox and Bad Maths in Courts This post is inspired by the recent BBC News article, "Amanda Knox and Bad Maths in Courts." The article highlights the importance of good mathematical understanding when handling probabilities - and how mistakes by judges and juries can sometimes lead to miscarriages of justice. A scenario to give to... Continue Reading →
Does it Pay to be Nice? Game Theory and Evolution Game theory is an interesting branch of mathematics with links across a large number of disciplines - from politics to economics to biology and psychology. The most well known example is that of the Prisoner's Dilemma. (Illustrated below). Two prisoners are taken into custody and... Continue Reading →
Is God a Mathematician? http://www.youtube.com/watch?v=jremlZvNDuk&feature=youtu.be That's the provocative question posed by American Physicist Michio Kaku in this fascinating 5 minute interview which takes in the ideas of Newton, Einstein and modern ideas on String Theory. It addresses the fundamental questions in maths ToK - is mathematics invented or discovered? What explains the "unreasonable effectiveness" of... Continue Reading →
Michio Kaku - American Professor of Theoretical Physics and fantastic populariser of mathematics and physics takes us through a 40 minute journey on the importance of physics in explaining the universe: http://www.youtube.com/watch?v=0NbBjNiw4tk Great stuff - well worth watching!
Graham's Number - literally big enough to collapse your head into a black hole Graham's Number is a number so big that it would literally collapse your head into a black hole were you fully able to comprehend it. And that's not hyperbole - the informational content of Graham's Number is so astronomically large that... Continue Reading →
Plus Maths has a large number of great podcasts which look at maths ToK topics: 1) An interview with Max Tegmark (pictured above) about why he thinks that the universe is itself a mathematical structure. 2) An interview with physicists David Berman about how many dimensions exist. 3) A talk with cosmologist John Barrow about... Continue Reading →
http://www.youtube.com/watch?v=PCu_BNNI5x4 What is the sum of the infinite sequence 1, -1, 1, -1, 1.....? This is a really interesting puzzle to study - which fits very well when studying geometric series, proof and the history of maths. The two most intuitive answers are either that it has no sum or that it sums to zero. ... Continue Reading →
There are some great telescope pictures of the universe on the Guardian Science Gallery this month. This picture shows the distorted remnants of a supernova explosion - where stars are destroyed. This particular supernova is 26,000 light years from Earth - meaning that this is a picture 26,000 years into the past. It is thought... Continue Reading →
This is a huge topic - closely related to some of the Theory of knowledge concepts. It also gets very complicated. Here are some of the basics (some of this information is simplified from the Stanford Encyclopedia which goes into far more detail). 1) Platonism The basic philosophical question in maths is ontological - ie concerned with... Continue Reading →
This is another fascinating branch of mathematics - which uses computing to illustrate complexity (and order) in nature. Langton's Ant shows how very simple initial rules (ie a deterministic system) can have very unexpected consequences. Langton's Ant follows two simple rules: 1) At a white square, turn 90° right, flip the color of the square,... Continue Reading →
Fermat's Theorem - one of the most famous and long running puzzles in mathematics is a great way to introduce proof, the history of mathematics and also to show how apparent work on an entirely abstract concept can actually drive the development of techniques which have real world applicability. The (much abridged!) story is that... Continue Reading →
Good at maths? Really good? Then maybe one day you'll be able to claim a $1million prize for solving some of the fiendishly difficult and important maths problems out there. In 2000, the Clay Institute offered the reward for any mathematician who was able to crack 7 mathematical problems. In 13 years only one of... Continue Reading →
A keyquestion in ToK is what can we know and what are the limits of our knowledge. Central to this, when it comes to the physical world, is the idea of chaos. Chaotic systems are those which are deterministic (ie. determined from initial conditions) and yet unpredictable - because small errors in approximating the initial state... Continue Reading →
Godel, a 20th century, Austrian American mathematician attempted to use the rigour of formal mathematical logic to provide a proof for the existence of God. Whilst somewhat daunting, a more simplified version can be regarded as, "God, by definition, is that for which no greater can be conceived. God exists in the understanding. If God... Continue Reading →
This formula above is one of the many staggering relationships found by mathematical genius Ramanujan - a largely self-taught Indian mathematician from around the turn of the 20th Century. It has been described by some mathematicians as Ramanujan's most beautiful formula - as it shows a remarkable connection between an infinite series, a continued fraction,... Continue Reading →
Fractals aren't actually on the syllabus - but they do offer quite a good opportunity to look at limits, infinite sequences, complex numbers (eg Julia sets etc), the relationship between maths and art and so on. This video is a fantastic introduction to fractals - looking at how the Koch snowflake has simultaneously a finite... Continue Reading →