Non Euclidean Geometry IV – New Universes

This post follows on from Non-Euclidean Geometry – An Introduction – read that one first! 

Non Euclidean Geometry IV – New Universes

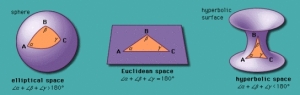
The 19th century saw mathematicians finally throw off the shackles of Euclid’s 5th (parallel) postulate – and go on to discover a bewildering array of geometries which no longer took this assumption about parallel lines as an axiomatic fact.

1) A curved space model

The surface of a sphere is a geometry where the parallel postulate does not hold.  This is because all straight lines in this geometry will meet.  We need to clarify what “straight” means in this geometry.  “Straight” lines are those lines defined to be of minimum distance from a to b on the surface of the sphere.  These lines therefore are defined by “great circles” which have the same radius as the sphere like those shown above.

A 2 dimensional being living on the surface of a 3D sphere would feel like he was travelling in a straight line from a to b when he was in fact travelling on the great circle containing both points.  He would not notice the curvature because the curvature would be occurring in the 3rd dimension – and as a 2 dimensional being he would not be able to experience this.

2) A field model –  Stereographic Projection for Riemann’s Sphere

A field model can be thought of in reverse.  A curved space model is a curved surface where straight lines are parts of great circles.  A field model is a flat surface where “straight lines” are curved.

This may seem rather strange, however, the German mathematician Riemann devised a way of representing every point on the sphere as a point on the plane.  He did this by first centering the sphere on the origin – as shown in the diagram above.  Next he took a point on the complex plane (z = x + iy ) and joined up this point to the North pole of the sphere (marked W).  This created a straight line which intersected the sphere at a single point at the surface of the sphere (say at z’).  Therefore every point on the sphere (z’) can be represented as a unique point on the plane (z) – in mathematical language, there is a one-to-one mapping between the two.

The only point on the sphere which does not equate to a point on the complex plane is that of the North pole itself (point w).  This is because no line touching w and another point on the sphere surface can ever reach the complex plane.  Therefore Riemann assigned the value of infinity to the North pole, and therefore the the sphere is a 1-1 mapping of all the points in the complex plane (and infinity).

On this field model (which is the flat complex plane), our straight lines are the stereographic projections of the great circles on the sphere.  As you can see from the sketch above, these projections will give us circles of varying sizes.  These are now our straight lines!

And this is where it starts to get really interesting – when we have two isometric spaces there is no way an inhabitant could actually know which one is his own reality.  A 2 dimensional being could be living in either the curved space model, or the field model and not know which was his true reality.

The difference between the 2 models is that in the first instance we accept an unexplained curvature of space that causes objects to travel in “straight” lines along great circles, and that in the second instance we accept an unexplained field which forces objects travelling in “straight” lines to follow curved paths.  Both of these ideas are fundamental to Einstein’s Theory of Relativity – where we must account for both the curvature of space-time and a gravitational force field.

Interestingly, our own 3 dimensional reality is isomorphic to the projection onto a 4 dimensional sphere (hypersphere) – and so our 3 dimensional universe is indistinguishable from a a curved 3D space which is the surface of a hypersphere.  A hypersphere may be a bit difficult to imagine, but the video above is about as close as we can get.

Such a scenario would allow for our space to be bounded rather than infinite, and for there to be an infinite number of 3D universes floating in the 4th dimension – each bounded by the surface of their own personal hypersphere.  Now that’s a bit more interesting than the Euclidean world of straight lines and circle theorems.

If you enjoyed this you might also like:

Non Euclidean Geometry V – The Shape of the Universe – the final part in the non-Euclidean Geometry series.

Imagining the 4th Dimension. How mathematics can help us explore the notion that there may be more than 3 spatial dimensions.

Geometry, Relativity and the Fourth Dimension is a fantastic (and very readable despite its daunting title!) book full of information about non-Euclidean geometry and extra dimensions.