Non Euclidean Geometry III – Breakthrough Into New Worlds

Non Euclidean Geometry – Spherical Geometry

This article follow on from Non Euclidean Geometry – An Introduction – read that first!

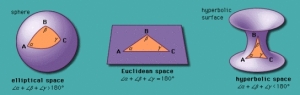
Most geometers up until the 19th century had focused on trying to prove that Euclid’s 5th (parallel) postulate was true.  The underlying assumption was that Euclidean geometry was true and therefore the 5th postulate must also be true.

The German mathematician Franz Taurinus made huge strides towards developing non-Euclidean geometries when in 1826 he published his work on spherical trigonometry.

Spherical trigonometry is a method of working out the sides and angles of triangles which are drawn on the surface of spheres.

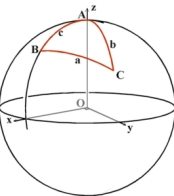
One of the fundamental formula for spherical trigonometry, for a sphere of radius k is:

cos(a/k) = cos(b/k).cos(c/k) + sin(b/k).sin(c/k).cosA

So, say for example we have a triangle as sketched above.  We know the radius of the sphere is 1, that the angle A = 60 degrees, the length b = 1, the length c =1, we can use this formula to find out what the length a is:

cos(a) = cos(1).cos(1) + sin(1).sin(1).cos60

a = 0.99996

We can note that for the same triangle sketched on a flat surface we would be able to use the formula:

a² = b² + c² – 2bc.cosA

a²= 1 + 1 – 2cos60

a = 1

Taurinus however wanted to investigate what would happen if the sphere had an imaginary radius (i).  Without worrying too much about what a sphere with an imaginary radius would look like, let’s see what this does to the previous spherical trigonometric equations:

The sphere now has a radius of ik where i = √-1, so:

cos(a/ik) = cos(b/ik).cos(c/ik) + sin(b/ik).sin(c/ik).cosA

But cos(ix) = cosh(x) and sin(ix) = (-1/i)sinh(x)  – where cosh(x) and sinh(x) are the hyperbolic trig functions.   So we can convert the above equation into:

cosh(a/k) = cosh(b/k)cosh(c/k) – sinh(b/k).sinh(c/k).cosA

This equation will give us the relationship between angles and sides on a triangle drawn on a sphere with an imaginary radius.

Now, here’s the incredible part – this new geometry based on an imaginary sphere (which Taurinus called Log-Spherical Geometry) actually agreed with the hypothesis of the acute angle  (the idea that triangles could have an angle sum less than 180 degrees).

Even more incredible, if you take the limit as k approaches infinity of this new equation, you are left with:

a² = b² + c² – 2bc.cosA

What does this mean?  Well, if we have a sphere of infinite imaginary radius it stretches and flattens to be indistinguishable from a flat plane – and this is where our normal Euclidean geometry works.  So, Taurinus had created a geometry for which our own Euclidean geometry is simply a special case.

So what other remarkable things happen in this new geometric world?  Well we have triangles that look like this:

This triangle has angle A = 0, angle C = 90 and lines AB and AC are parallel, (they never meet).  This sketch introduces a whole new concept of parallelism far removed from anything Euclid had imagined. The angle  β is called the angle of parallelism – and measures the angle between a perpendicular and parallel line.  Unlike in Euclidean geometry this angle does not have to be 90 degrees.  Indeed the angle  β will now change as we move the perpendicular along AC – as it is dependent on the length of the line a.

So, we are now into some genuinely weird and wonderful realms where normal geometry no longer makes sense.  Be warned – it gets even stranger!  More on that in the next post.

If you enjoyed this post you might also like:

Non Euclidean Geometry IV – New Universes – The fourth part in the non-Euclidean Geometry series.

The Riemann Sphere – The Riemann Sphere is a way of mapping the entire complex plane onto the surface of a 3 dimensional sphere.

Circular Inversion – Reflecting in a Circle The hidden geometry of circular inversion allows us to begin to understand non-Euclidean geometry.