IB Maths Resources from Intermathematics
IB Maths Resources: 300 IB Maths Exploration ideas, video tutorials and Exploration Guides
https://www.youtube.com/watch?v=nlm07asSU0c Winning at Snakes and Ladders The fantastic Marcus de Sautoy has just made a video on how to use Markov chains to work out how long it will take to win at Snakes and Ladders. This uses a different method to those I've explored before (Playing Games with Markov Chains) so it's well worth... Continue Reading →
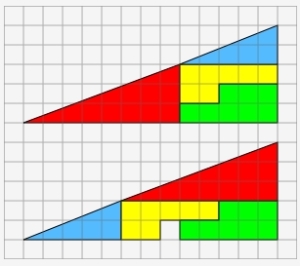
Proving Pythagoras Like Einstein? There are many ways to prove Pythagoras' theorem - Einstein reputedly used the sketch above to prove this using similar triangles. To keep in the spirit of discovery I also just took this diagram as a starting point and tried to prove this myself, (though Einstein's version turns out to be... Continue Reading →
https://www.youtube.com/watch?v=i4VqXRRXi68 Find the average distance between 2 points on a square This is another excellent mathematical puzzle from the MindYourDecisions youtube channel. I like to try these without looking at the answer - and then to see how far I get. This one is pretty difficult (and the actual solution exceptionally difficult!) The problem is... Continue Reading →
Further investigation of the Mordell Equation This post carries on from the previous post on the Mordell Equation - so make sure you read that one first - otherwise this may not make much sense. The man pictured above (cite: Wikipedia) is Louis Mordell who studied the equations we are looking at today (and which... Continue Reading →
The Mordell Equation [Fermat's proof] Let's have a look at a special case of the Mordell Equation, which looks at the difference between an integer cube and an integer square. In this case we want to find all the integers x,y such that the difference between the cube and the square gives 2. These sorts... Continue Reading →
Hollow Cubes investigation Hollow cubes like the picture above [reference] are an extension of the hollow squares investigation done previously. This time we can imagine a 3 dimensional stack of soldiers, and so try to work out which numbers of soldiers can be arranged into hollow cubes. Therefore what we need to find is what... Continue Reading →
Waging war with maths: Hollow squares The picture above [US National Archives, Wikipedia] shows an example of the hollow square infantry formation which was used in wars over several hundred years. The idea was to have an outer square of men, with an inner empty square. This then allowed the men in the formation to... Continue Reading →
https://www.youtube.com/watch?v=5TkIe60y2GI Normal Numbers - and random number generators Numberphile have a nice new video where Matt Parker discusses all different types of numbers - including "normal numbers". Normal numbers are defined as irrational numbers for which the probability of choosing any given 1 digit number is the same, the probability of choosing any given 2... Continue Reading →
Volume optimization of a cuboid This is an extension of the Nrich task which is currently live - where students have to find the maximum volume of a cuboid formed by cutting squares of size x from each corner of a 20 x 20 piece of paper. I'm going to use an n x 10 rectangle... Continue Reading →
https://www.youtube.com/watch?v=4aMtJ-V26Z4 Narcissistic Numbers Narcissistic Numbers are defined as follows: An n digit number is narcissistic if the sum of its digits to the nth power equal the original number. For example with 2 digits, say I choose the number 36: 32 + 62 = 45. Therefore 36 is not a narcissistic number, as my answer... Continue Reading →
This is a nice example of using some maths to solve a puzzle from the mindyourdecisions youtube channel (screencaptures from the video). How to Avoid The Troll: A Puzzle In these situations it's best to look at the extreme case first so you get some idea of the problem. If you are feeling particularly pessimistic... Continue Reading →
http://www.youtube.com/watch?v=skM37PcZmWE Zeno's Paradox - Achilles and the Tortoise This is a very famous paradox from the Greek philosopher Zeno - who argued that a runner (Achilles) who constantly halved the distance between himself and a tortoise would never actually catch the tortoise. The video above explains the concept. There are two slightly different versions to... Continue Reading →
A geometric proof for the Arithmetic and Geometric Mean There is more than one way to define the mean of a number. The arithmetic mean is the mean we learn at secondary school - for 2 numbers a and b it is: (a + b) /2. The geometric mean on the other hand is defined... Continue Reading →
This is an example of how an investigation into area optimisation could progress. The problem is this: A farmer has 40m of fencing. What is the maximum area he can enclose? Case 1: The rectangle: Reflection - the rectangle turns out to be a square, with sides 10m by 10m. Therefore the area enclosed is... Continue Reading →
Sequence Investigation This is a nice investigation idea from Nrich. The above screen capture is from their Picture Story puzzle. We have successive cubes - a 1x1x1 cube, a 2x2x2 cube etc. The cubes are then rearranged to give the following shape. The puzzle is then to use this information to discover a mathematical relationship.... Continue Reading →
This is a great puzzle which the Guardian ran last week: Fill in the equations below using any of the basic mathematical operations, +, –, x, ÷, and as many brackets as you like, so that they make arithmetical sense. 10 9 8 7 6 5 4 3 2 1 = 2017 There are many... Continue Reading →
The Watson Selection Task - a logical puzzle The Watson Selection Task is a logical problem designed to show how bad we are at making logical decisions. Watson first used it in 1968 - and found that only 10% of the population would get the correct answer. Indeed around 65% of the population make the... Continue Reading →
This is a nice example of using some maths to solve a puzzle from the mindyourdecisions youtube channel (screencaptures from the video). How to Avoid The Troll: A Puzzle In these situations it's best to look at the extreme case first so you get some idea of the problem. If you are feeling particularly pessimistic... Continue Reading →
This is a classic puzzle which is discussed in some more detail by the excellent Wired article. The puzzle is best represented by the picture below. We have a hunter who whilst in the jungle stumbles across a monkey on a tree branch. However he knows that the monkey, being clever, will drop from the branch... Continue Reading →
https://www.youtube.com/watch?v=rudzYPHuewc How to Win at Rock, Paper, Scissors You might think that winning at rock, paper, scissors was purely a matter of chance - after all mathematically each outcome has the same probability. We can express the likelihood of winning in terms of a game theory grid: It is clear that in theory you would... Continue Reading →
Can you find a sequence of consecutive integers that add up to 1000? This puzzle is based on the excellent book A First Step to Mathematical Olympiad Problems - which is full of problems that could be extended to become exploration ideas. Step 1 - arithmetic formula Our first step is to write out what... Continue Reading →
Tetrahedral Numbers - Stacking Cannonballs This is one of those deceptively simple topics which actually contains a lot of mathematics - and it involves how spheres can be stacked, and how they can be stacked most efficiently. Starting off with the basics we can explore the sequence: 1, 4, 10, 20, 35, 56.... These are... Continue Reading →
Hailstone Numbers This is a post inspired by the article on the same topic by the ever brilliant Plus Maths. Hailstone numbers are created by the following rules: if n is even: divide by 2 if n is odd: times by 3 and add 1 We can then generate a sequence from any starting number. ... Continue Reading →
Stellar Numbers Investigation This is an old IB internal assessment question and so can not be used for the new IB exploration - however it does give a good example of the sort of pattern investigation that is possible. The task starts off with the fairly straightforward problem of trying to find the nth term... Continue Reading →
Maths Puzzles These should all be accessible for top sets in KS4 and post 16. See if you can manage to get all 3 correct. Puzzle Number 1 Why is xx undefined when x = 0 ? Puzzle Number 2 I multiply 3 consecutive integers together. My answer is 8 times the middle of the... Continue Reading →
http://www.youtube.com/watch?v=w-I6XTVZXww Analytic Continuation and the Riemann Zeta Function Analytic Continuation is a very important mathematical technique which allows us to extend the domain of functions. It is essential in higher level mathematics and physics and leads to some remarkable results. For example, by using analytic continuation we can prove that the sum of the natural... Continue Reading →
Murder in the Maths Department A murder has been committed in the maths department! A body has been discovered surrounded by mathematical objects and only the hardworking maths teachers were in school, doing long division sums for fun at the weekend. One of them must be the murderer. (The wall of fame of successful detectives... Continue Reading →
https://www.youtube.com/watch?v=UK8Y_FDyDbg The Poincare Conjecture and Grigori Perelman In 2006 the Russian mathematician Grigori Perelman was awarded the mathematical equivalent of the mathematical Nobel prize (the Fields Medal). He declined it. In 2010 he was the first mathematician to be awarded $1 million - he turned it down. What had Perelman done to achieve such (apparently... Continue Reading →
http://www.youtube.com/watch?v=skM37PcZmWE Zeno's Paradox - Achilles and the Tortoise This is a very famous paradox from the Greek philosopher Zeno - who argued that a runner (Achilles) who constantly halved the distance between himself and a tortoise would never actually catch the tortoise. The video above explains the concept. There are two slightly different versions to... Continue Reading →
The Telephone Numbers - Graph Theory The telephone numbers are the following sequence: 1, 1, 2, 4, 10, 26, 76, 232, 764, 2620, 9496... (where we start from n=0). This pattern describes the total number of ways which a telephone exchange with n telephones can place a connection between pairs of people. To illustrate this... Continue Reading →
Happy Numbers Happy numbers are defined by the rule that you start with any positive integer, square each of the digits then add them together. Now do the same with the new number. Happy numbers will eventually spiral down to a number of 1. Numbers that don't eventually reach 1 are called unhappy numbers. As... Continue Reading →
This is inspired from the great site, Practical Cryptography which is a really good resource for code making and code breaking. One of their articles is about how we can use the Chi Squared test to crack a Caesar Shift code. Indeed, if you use an online program to crack a Caesar shift, they are... Continue Reading →
Code Breakers Wanted by the NSA The American National Security Agency have just launched a new code breaking challenge. The tweet above is the first in their series for those interested in a career in code breaking. The NSA are possibly in search of some good publicity after the revelations of Edward Snowden with... Continue Reading →
http://www.youtube.com/watch?v=w-I6XTVZXww Unbelievable: 1+2+3+4.... = -1/12 ? The above video by the excellent team at Numberphile has caused a bit of an internet stir - by providing a proof that 1+2+3+4+5+... = -1/12 It's well worth watching as an example of what proof means - if something is proved which we "know" is wrong, then should... Continue Reading →
Visualising Algebra Through Geometry This picture above is a fantastic example of how we can use geometry to visualise an algebraic expression. It's taken from Brilliant - which is a fantastic new forum for sharing maths puzzles. This particular puzzle was created and uploaded by Arron Kau. The question is, which of the following mathematical... Continue Reading →
Fermat's Theorem on the sum of two squares Not as famous as Fermat's Last Theorem (which baffled mathematicians for centuries), Fermat's Theorem on the sum of two squares is another of the French mathematician's theorems. Fermat asserted that all odd prime numbers p of the form 4n + 1 can be expressed as: where x... Continue Reading →
e's are good - He's Leonard Euler. Along with pi, e is one of the most important constants in mathematics. It is an irrational number which carries on forever. The first few digits are 2.718281828459045235... Leonard Euler e is sometime named after Leonard Euler (Euler’s number). He wasn't the first mathematician to discover e -... Continue Reading →
https://www.youtube.com/watch?v=t8XMeocLflc This classic clip "proves" how 25/5 = 14, and does it three different ways. Maths is a powerful method for providing proof - but we need to be careful that each step is based on correct assumptions. One of the most well known fake proofs is as follows: let a = b Then a2... Continue Reading →
Game Theory and Tic Tac Toe The game of Noughts and Crosses or Tic Tac Toe is well known throughout the world and variants are thought to have been played over 2000 years ago in Rome. It's a very simple game - the first person to get 3 in a row wins. In fact it's... Continue Reading →
Maths and Chess Magnus Carlsen, the 22 year old chess prodigy from Norway (pictured above), has just been crowned World Chess Champion, winning £1.4 million in the process. He beat the Indian Grandmaster Vishy Anand in a 12 match series in India with 2 games to go. Anand has been the World Champion since 2007... Continue Reading →
The Knight's Tour is a mathematical puzzle that has endured over 1000 years. The question is simple enough - a knight (which can move as illustrated above) wants to visit all the squares on a chess board only once. What paths can it take? You can vary the problem by requiring that the knight starts... Continue Reading →
http://www.youtube.com/watch?v=a2ey9a70yY0 The Birthday Problem One version of the birthday problem is as follows: How many people need to be in a room such that there is a greater than 50% chance that 2 people share the same birthday. This is an interesting question as it shows that probabilities are often counter-intuitive. The answer is that... Continue Reading →
The Goldbach Conjecture is one of the most famous problems in mathematics. It has remained unsolved for over 250 years - after being proposed by German mathematician Christian Goldbach in 1742. Anyone who could provide a proof would certainly go down in history as one of the true great mathematicians. The conjecture itself is deceptively... Continue Reading →
http://www.youtube.com/watch?v=VIVIegSt81k Hexaflexagons - Amazing Shapes Investigation: Hexaflexagons look at first glance to be somewhat prosaic origami shapes - but like mobius strips they hide some surprises. Flexagons are paper shapes that can be folded to reveal hidden faces - and hexaflexagons themselves have six sides. What's remarkable about hexaflexagons is that during folding, some faces... Continue Reading →
Cracking RSA Code - The World's Most Important Code? RSA code is the basis of all important data transfer. Encrypted data that needs to be sent between two parties, such as banking data or secure communications relies on the techniques of RSA code. RSA code was invented in 1978 by three mathematicians (Rivest, Shamir and... Continue Reading →
GCHQ - the British cyber spy agency - have had a rough few months following some staggering revelations from Edward Snowden, so they're doing some positive PR at the moment to highlight the importance of mathematics and computing skills in code-breaking. There are 4 codes to solve (the first one posted above) - each answer... Continue Reading →
https://www.youtube.com/watch?v=M4vqr3_ROIk The video above is a great example of "mathemagic" - magic through maths. Arthur Benjamin's show at TED (using a mixture of mathematical tricks and savant like numerical ability) shows how numerical calculations can still produce a sense of awe and wonder. Probably the best resource for "mathemagic" is the TES Word ebook from... Continue Reading →
A Maths Snooker Puzzle This was suggested by Paul our Physics teacher - and is a nice little maths puzzle. The maximum break score in snooker is 147 which is achieved by: 15 reds (1 point each) , 15 blacks (7 points each), then yellow ( 2 points), then green (3 points), brown (4 points), blue... Continue Reading →
Cracking Codes Lesson 1 Introduction: 5 minutes - Use a Morse Code Generator to play some (very slowed down) messages for students to decode. Discuss why this is was a good way to transmit data in the past. Brainstorm: 5 minutes – Why are codes important? Who uses them? Why do mathematicians go into this career? ... Continue Reading →
Wau: The Most Amazing Number in the World? This is a fantastic video from Vi Hart of Khan Academy. Watch it first and marvel at the properties of this amazing number: https://www.youtube.com/watch?feature=player_embedded&v=GFLkou8NvJo Once you have watched it, watch it again - this time thinking about what number Wau might be - and why you have... Continue Reading →