Narcissistic Numbers

If you are a teacher then please also visit my new site: intermathematics.com for over 2000+ pdf pages of resources for teaching IB maths!

Narcissistic Numbers

Narcissistic Numbers are defined as follows:

An n digit number is narcissistic if the sum of its digits to the nth power equal the original number.

For example with 2 digits, say I choose the number 36:

3² + 6² = 45. Therefore 36 is not a narcissistic number, as my answer is not 36.

For example with 3 digits, say I choose the number 124:

1³ + 2³ + 4³ = 73. Therefore 124 is not a narcissistic number as my answer is not 124.

The question is how to find all the narcissistic numbers less than 1000, without checking 1000 different numbers? Let’s start with 1 digit numbers.

1 digit numbers

0¹ = 0
1¹ = 1
2¹ = 2 etc.

Therefore all numbers from 0-9 are narcissistic.

2 digit numbers

For 2 digit numbers in the form ab we need the following:

a² + b² = 10a + b.

Therefore

a² – 10a + b² – b = 0.

Next if we choose a = 1,2,3,4,5 we get the following simultaneous equations:

b² – b -16 = 0

b² – b -21 = 0

b² – b -24 = 0

b² – b -25 = 0

None of these factorise for integer solutions, therefore there are no 2 digit solutions from 11 to 59. Trying a = 6,7,8,9 we find that we get the same as the first four equations. This is because a and 10-a give equivalent solutions. In other words, when a = 1 we get the equation b² – b -9 = 0 and when a = 9 we also get the equation b² – b -9 = 0. This is because:

for:

a² – 10a

if we substitute a = (10 – a) we get

(10 – a)² – 10(10 – a) = a² – 10a.

Therefore we prove that there are no 2 digit narcissistic numbers.

3 digit numbers

First we list the cube numbers:

1³ = 1, 2³ = 8, 3³ = 27, 4³ = 64, 5³ = 125, 6³ = 216, 7³ = 343, 8³ = 512, 9³ = 729.

and then consider 3 digit numbers of the form 1bc first. We need:

1³+ b³ + c³ = 100 + 10b + c.

If our first digit is 1, then b³ + c³ need to add up to give us a number in the one hundreds, therefore:

99 ≤  b³ + c³≤ 198.

We can then check the cube numbers and see that the only possible combinations for a and b are 0 5, 5 0, 1 5, 5 1, 2 5, 5 2, 3 5, 5 3, 4 4, 4 5, 5 4. We can check these (only have to use the calculator for half as the reversed numbers give equivalent answers) and find that for 153 we do indeed get a narcissistic number i.e:

1³+ 5³ + 3³ = 153.

Next we consider 3 digit numbers of the form 2bc first. We need:

192 ≤  b³ + c³≤ 292

This gives the following possibilities for b and c: 6 0, 0 6, 6 1, 16, 2 6, 6 2, 6 3, 3 6, 6 4, 4 6.

None of these give narcissistic numbers.

Next we consider 3 digit numbers of the form 3bc first. We need:

273 ≤  b³ + c³≤373

This gives the following possibilities for b and c: 6 4, 4 6, 6 5, 5 6, 7 1, 1 7, 7 2, 2 7, 7 3, 3 7, 7 0, 0 7.

Checking these we find 2 more narcissistic numbers:

370 = 3³+ 7³ + 0³

371= 3³+ 7³ + 1³

Using the same method, we can find that the only possibilities for 4bc are: 5 6, 6 5, 7 1, 1 7, 7 2, 2 7, 7 3, 3 7, 7 4, 4 7, 7 0, 0 7.  Checking these gives us 1 more narcissistic number:

407= 4³+ 0³ + 7³

We can carry on with this method checking up to the form 9ab (it gets easier as there are less combinations possible, but will find no more narcissistic numbers.  Therefore we have all the narcissistic numbers less than 1000:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407.

Is there a limit to how many narcissistic numbers there are?

Surprisingly there is a limit – there are exactly 88 narcissistic numbers in base 10. To see why we can consider the following:

In 3 digits the biggest number we can choose is 999. That would give 9³+ 9³ + 9³ (or 3(9)³). This needs to give a number in the hundreds (10²) otherwise it would be impossible to achieve a narcissistic number. Therefore with an n digit number the largest number we can make is n(9)ⁿ and if we can’t make a number in the 10^n-1, then a narcissistic number is not possible. If we can prove that the inequality:

n(9)ⁿ < 10^n-1

is true for some values of n, then there will be an upper bound to the narcissistic numbers we can make. We could simply plot this directly, but let’s see if we can convince ourselves it’s true for some n without using graphical software first. Let’s see if we can find an equality:

n(9)ⁿ = 10^n-1

First we take log base 10 of both sides

log n(9)ⁿ = n-1

log(n) + nlog(9) = n-1

n(log9 -1) + logn +1 = 0

Next we make the substitution logn = u and therefore 10^u = n. This gives:

10^u(log9 -1) + u + 1 = 0.

Now we can clearly see that 10^u will grow much larger than u + 1, so any root must be for u is small. Let’s see, when u = 1 we get a positive number (as log9 -1 is a negative number close to 0), but when u = 2 we get a negative number. Therefore we have a root between u = 1 and u = 2. Given that we made the substitution logn = u, that means we have found the inequality n(9)ⁿ < 10^n-1 will hold for n somewhere between 10¹ and 10 ².

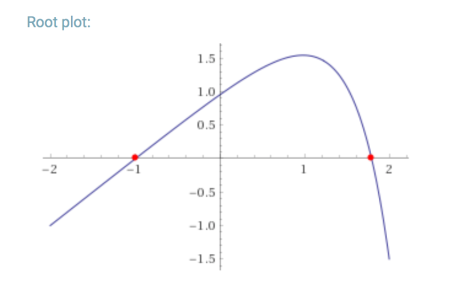
Using Wolfram we can see that the equality is reached when u = 1.784, i.e when n = 10^1.784 or approx 60.8. Therefore we can see that when we have more than 60 digit numbers, it is no longer possible to make narcissistic numbers.
Essential Resources for IB Teachers

1) Intermathematics.com

If you are a teacher then please also visit my new site.  This has been designed specifically for teachers of mathematics at international schools.  The content now includes over 2000 pages of pdf content for the entire SL and HL Analysis syllabus and also the SL Applications syllabus.  Some of the content includes:

1. Original pdf worksheets (with full worked solutions) designed to cover all the syllabus topics.  These make great homework sheets or in class worksheets – and are each designed to last between 40 minutes and 1 hour.
2. Original Paper 3 investigations (with full worked solutions) to develop investigative techniques and support both the exploration and the Paper 3 examination.
3. Over 150 pages of Coursework Guides to introduce students to the essentials behind getting an excellent mark on their exploration coursework.
4. A large number of enrichment activities such as treasure hunts, quizzes, investigations, Desmos explorations, Python coding and more – to engage IB learners in the course.

There is also a lot more.  I think this could save teachers 200+ hours of preparation time in delivering an IB maths course – so it should be well worth exploring!

Essential Resources for both IB teachers and IB students

1) Exploration Guides and Paper 3 Resources

I’ve put together a 168 page Super Exploration Guide to talk students and teachers through all aspects of producing an excellent coursework submission.  Students always make the same mistakes when doing their coursework – get the inside track from an IB moderator!  I have also made Paper 3 packs for HL Analysis and also Applications students to help prepare for their Paper 3 exams.  The Exploration Guides can be downloaded here and the Paper 3 Questions can be downloaded here.