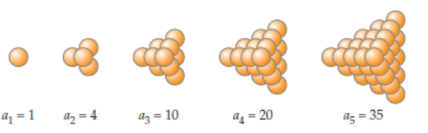IB Maths Resources from Intermathematics
IB Maths Resources: 300 IB Maths Exploration ideas, video tutorials and Exploration Guides
Maths and Evolutionary Biology Mathematics is often utilised across many fields - lets look at an example from biology, evolutionary biology and paleontology, in trying to understand the development of homo-sapiens. We can start with a large data set which gives us the data for mammal body mass and brain size in grams (downloaded from... Continue Reading →
Time dependent gravity exploration In our universe we have a gravitational constant - i.e gravity is not dependent on time. If gravity changed with respect to time then the gravitational force exerted by the Sun on Earth would lessen (or increase) over time with all other factors remaining the same. Interestingly time-dependent gravity was first... Continue Reading →
Finding planes with radar PlusMaths recently did a nice post about the link between ellipses and radar (here), which inspired me to do my own mini investigation on this topic. We will work in 2D (with planes on the ground) for ease of calculations! A transmitter will send out signals - and if any of... Continue Reading →
What is the average distance between 2 points in a rectangle? Say we have a rectangle, and choose any 2 random points within it. We then could calculate the distance between the 2 points. If we do this a large number of times, what would the average distance between the 2 points be? Monte Carlo... Continue Reading →
Life on the Beach with Markov Chains Markov chains are exceptionally useful tools for calculating probabilities - and are used in fields such as economics, biology, gambling, computing (such as Google's search algorithm), marketing and many more. They can be used when we have the probability of a future event dependent on a current event.... Continue Reading →
Anscombe's Quartet - the importance of graphs! Anscombe's Quartet was devised by the statistician Francis Anscombe to illustrate how important it was to not just rely on statistical measures when analyzing data. To do this he created 4 data sets which would produce nearly identical statistical measures. The scatter graphs above generated by the Python... Continue Reading →
Generating e through probability and hypercubes This is a really beautiful solution to an interesting probability problem posed by fellow IB teacher Daniel Hwang, for which I've outlined a method for solving suggested by Ferenc Beleznay. The problem is as follows: On average, how many random real numbers from 0 to 1 (inclusive) are required... Continue Reading →
3D Printing with Desmos: Stewie Griffin Using Desmos or Geogebra to design a picture or pattern is quite a nice exploration topic - but here's an idea to make your investigation stand out from the crowd - how about converting your image to a 3D printed design? Step 1 Create an image on Desmos or... Continue Reading →
Time dependent gravity and cosmology! In our universe we have a gravitational constant - i.e gravity is not dependent on time. If gravity changed with respect to time then the gravitational force exerted by the Sun on Earth would lessen (or increase) over time with all other factors remaining the same. Interestingly time-dependent gravity was... Continue Reading →
https://www.youtube.com/watch?v=Ry3B9hJbBfk The Martingale system The Martingale system was first used in France in 1700s gambling halls and remains used today in some trading strategies. I'll look at some of the mathematical ideas behind this and why it has remained popular over several centuries despite having a long term expected return of zero. The scenario You... Continue Reading →
Projectiles IV: Time dependent gravity! This carries on our exploration of projectile motion - this time we will explore what happens if gravity is not fixed, but is instead a function of time. (This idea was suggested by and worked through by fellow IB teachers Daniel Hwang and Ferenc Beleznay). In our universe we... Continue Reading →
Using Maths to model the spread of Coronavirus (COVID-19) This coronavirus is the latest virus to warrant global fears over a disease pandemic. Throughout history we have seen pandemic diseases such as the Black Death in Middle Ages Europe and the Spanish Flu at the beginning of the 20th century. More recently we have seen... Continue Reading →
Finding the volume of a rugby ball (prolate spheroid) With the rugby union World Cup currently underway I thought I'd try and work out the volume of a rugby ball using some calculus. This method works similarly for American football and Australian rules football. The approach is to consider the rugby ball as an... Continue Reading →
Soap Bubbles and Catenoids Soap bubbles form such that they create a shape with the minimum surface area for the given constraints. For a fixed volume the minimum surface area is a sphere, which is why soap bubbles will form spheres where possible. We can also investigate what happens when a soap film is formed... Continue Reading →
https://www.youtube.com/watch?v=etMJxB-igrc The Van Eck Sequence This is a nice sequence as discussed in the Numberphile video above. There are only 2 rules: If you have not seen the number in the sequence before, add a 0 to the sequence. If you have seen the number in the sequence before, count how long since you... Continue Reading →
Computers can brute force a lot of simple mathematical problems, so I thought I'd try and write some code to solve some of them. In nearly all these cases there's probably a more elegant way of coding the problem - but these all do the job! You can run all of these with a Python... Continue Reading →
https://www.youtube.com/watch?v=q6L06pyt9CA Stacking cannonballs - solving maths with code Numberphile have recently done a video looking at the maths behind stacking cannonballs - so in this post I'll look at the code needed to solve this problem. Triangular based pyramid. A triangular based pyramid would have: 1 ball on the top layer 1 + 3 balls... Continue Reading →
Volume optimization of a cuboid This is an extension of the Nrich task which is currently live - where students have to find the maximum volume of a cuboid formed by cutting squares of size x from each corner of a 20 x 20 piece of paper. I'm going to use an n x 10 rectangle... Continue Reading →
Modeling hours of daylight Desmos has a nice student activity (on teacher.desmos.com) modeling the number of hours of daylight in Florida versus Alaska - which both produce a nice sine curve when plotted on a graph. So let's see if this relationship also holds between Phuket and Manchester. First we can find the daylight hours... Continue Reading →
This is a nice example of using some maths to solve a puzzle from the mindyourdecisions youtube channel (screencaptures from the video). How to Avoid The Troll: A Puzzle In these situations it's best to look at the extreme case first so you get some idea of the problem. If you are feeling particularly pessimistic... Continue Reading →
The Folium of Descartes The folium of Descartes is a famous curve named after the French philosopher and mathematician Rene Descartes (pictured top right). As well as significant contributions to philosophy ("I think therefore I am") he was also the father of modern geometry through the development of the x,y coordinate system of plotting algebraic... Continue Reading →
Spotting Asset Bubbles Asset bubbles are formed when a service, product or company becomes massively over-valued only to crash, taking with it most of its investors' money. There are many examples of asset bubbles in history - the Dutch tulip bulb mania and the South Sea bubble are two of the most famous historical examples.... Continue Reading →
https://www.youtube.com/watch?v=KfAs2hztDtI Measuring the Distance to the Stars This is a very nice example of some very simple mathematics achieving something which for centuries appeared impossible - measuring the distance to the stars. Before we start we need a few definitions: 1 Astronomical Unit (AU) is the average distance from the Sun to the Earth. This... Continue Reading →
The Rise of Bitcoin Bitcoin is in the news again as it hits $10,000 a coin - the online crypto-currency has seen huge growth over the past 1 1/2 years, and there are now reports that hedge funds are now investing part of their portfolios in the currency. So let's have a look at... Continue Reading →
This is a quick example of how using Tracker software can generate a nice physics-related exploration. I took a spring, and attached it to a stand with a weight hanging from the end. I then took a video of the movement of the spring, and then uploaded this to Tracker. Height against time The first... Continue Reading →
Predicting the UK election using linear regression The above data is the latest opinion poll data from the Guardian. The UK will have (another) general election on June 8th. So can we use the current opinion poll data to predict the outcome? Longer term data trends Let's start by looking at the longer term trend... Continue Reading →
Modelling a Nuclear War With the current saber rattling from Donald Trump in the Korean peninsula and the instability of North Korea under Kim Jong Un (incidentally a former IB student!) the threat of nuclear war is once again in the headlines. Post Cold War we've got somewhat used to the peace afforded by the... Continue Reading →
Simulations -Traffic Jams and Asteroid Impacts Why do traffic jams form? How does the speed limit or traffic lights or the number of lorries on the road affect road conditions? You can run a number of different simulations - looking at ring road traffic, lane closures and how robust the system is by applying an... Continue Reading →
Maths of Global Warming - Modeling Climate Change The above graph is from NASA's climate change site, and was compiled from analysis of ice core data. Scientists from the National Oceanic and Atmospheric Administration (NOAA) drilled into thick polar ice and then looked at the carbon content of air trapped in small bubbles in the... Continue Reading →