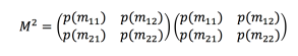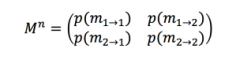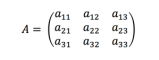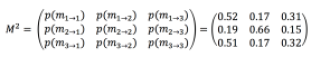Life on the Beach with Markov Chains

Life on the Beach with Markov Chains

Markov chains are exceptionally useful tools for calculating probabilities – and are used in fields such as economics, biology, gambling, computing (such as Google’s search algorithm), marketing and many more.  They can be used when we have the probability of a future event dependent on a current event.  The image above is of the Russian mathematician Andrey Markov [public domain picture from here] who was the first mathematician to work in this field (in the late 1800s).

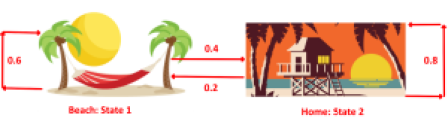
Beach life

The picture above is an example of a situation which can be modeled using a Markov chain.  We have two states:  Beach (state 1) and Home (state 2).  In our happy life we spend all the hours of the day in either one of these two states.  If we are on the beach then the probability we remain on the beach in one hour is 0.6 and the probability we go home in one hour is 0.4.  If we are at home the probability we remain at home in one hour is 0.8 and the probability we go to the beach is 0.2.  Hopefully you can see how this information is represented above.

Using matrices

First we need to represent our information in a matrix form.  A general 2×2 matrix is written as:

Where the subscript tells you the row and column (e.g. a_12 tells you it is in the first row and 2nd column).

For our Markov chain we define the following matrix:

Here m_11 is the situation of starting in state 1 and moving to state 1.  m_12 is the situation of starting in state 1 and moving to state 2.  Therefore p(m_12) is the probability of starting in state 1 and moving to state 2.  So for our beach  existence we have:

The 0.6 shows that if we are already on the beach we have a 0.6 chance of still being on the beach in one hour.

Where will we be in the future?

The benefit of Markov chains is that they allow us to utilise computer power to now calculate where someone will be in the future – simply by taking the power of the matrix.  To find the probabilities after 2 hours I can square my matrix:

Using the rules of matrix multiplication this then gives:

Which we can the calculate as:

I’ve used arrow notation here to represent the start and end state so p(m_1 arrow 1) means starting at 1 and ending at 1 after 2 hours.  We can see that for someone who started in the beach, the chance of them being on the beach in 2 hours is 0.44.  Equally the probability of someone who started in the house being on the beach in 2 hours is 0.28.

I can then carry on with matrix multiplication to work out where someone will likely be for any given number of hours in the future.  

p(m_1 arrow 1) means starting at 1 and ending at 1 after n hours.  So for example if I want to see where someone will be in 24 hours I simply do:

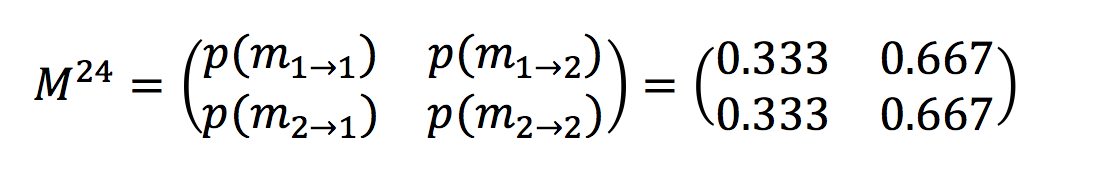
We can see that now it doesn’t actually matter (to 3sf anyway) where someone started – if they started on the beach there is a 0.333 chance they are on the beach in 24 hours, if they started in the house there is also a 0.333 chance they are on the beach in 24 hours.  So I can conclude that as the number of hours increase towards infinity that the person in this scenario would spend 1/3 of their time on the beach and 2/3 of their time at home – not a bad life!

A more demanding beach life

We can see that things get much more complicated, even by adding an extra state.  Now we have 3 possible states, Beach (state 1), Home (state 2) and SCUBA (state 3).  This time we need a 3×3 matrix:

and as before we define our probability matrix as:

So from our diagram we have the following:

For example the 0.8 in row 2 column 2 shows that there is a 0.8 chance of starting in state 2 (Home) and ending in state 2 (Home) in one hour.

Then using our same notation we have:

Which shows that after 2 hours there is (for example) a 0.19 chance that someone who started in state 2 (Home) is now found in state 1 (Beach).

After 24 hours we have the following matrix:

So we notice the same situation as last time – as the number of hours increase it gets less important where we started from – we can see that to 3sf it doesn’t now matter where we started – the probability after 24 hours of being found on the beach is 0.407, the probability of being found at home is 0.333 and the probability of being found diving is 0.260.

Hopefully this is a quick example to demonstrate the power of Markov chains in working with probabilities.  There is a lot more to explore (maybe in another post!)