Maths Games and Markov Chains

Maths Games and Markov Chains

This post carries on from the previous one on Markov chains – be sure to read that first if this is a new topic.  The image above is of the Russian mathematician Andrey Markov [public domain picture from here] who was the first mathematician to work in this field (in the late 1800s).

Creating a maths game

Above I have created a simple maths game – based on the simplified rules of Monopoly.  All players start at Go.  All players roll 2 dice and add the scores and move that number of squares forward (after square 9 you move to square 1 etc).  If you roll a double you get sent to Jail (square 9) – but are released on your next turn.  If you land on square 5 you immediately are transported to Go (and end your turn).  

The question is, if we play this game over the long run which famous mathematician will receive the most visits?  (In order we have Newton (2), Einstein (3), Euler (4), Gauss (6), Euclid (7), Riemann (8)).

Creating a Markov Chain

The first task is to work out the probabilities of landing on each square for someone who is starting on any square.  Using a sample space diagram you can work out the following:

p(move 2) = 0.  p(move 3) = 2/36.  p(move 4) = 2/36.  p(move 5) = 4/36.  p(move 6) = 4/36.  p(move 7) = 6/36.  p(move 8) = 4/36.  p(move 9) = 4/36.  p(move 10) = 2/36.  p(move 11) = 2/36. p(move 12) = 0.  p(double) = 6/36.

We can see that the only variation from the standard sample space is that we have separated the doubles – because they will move us to jail.  

Matrix representation

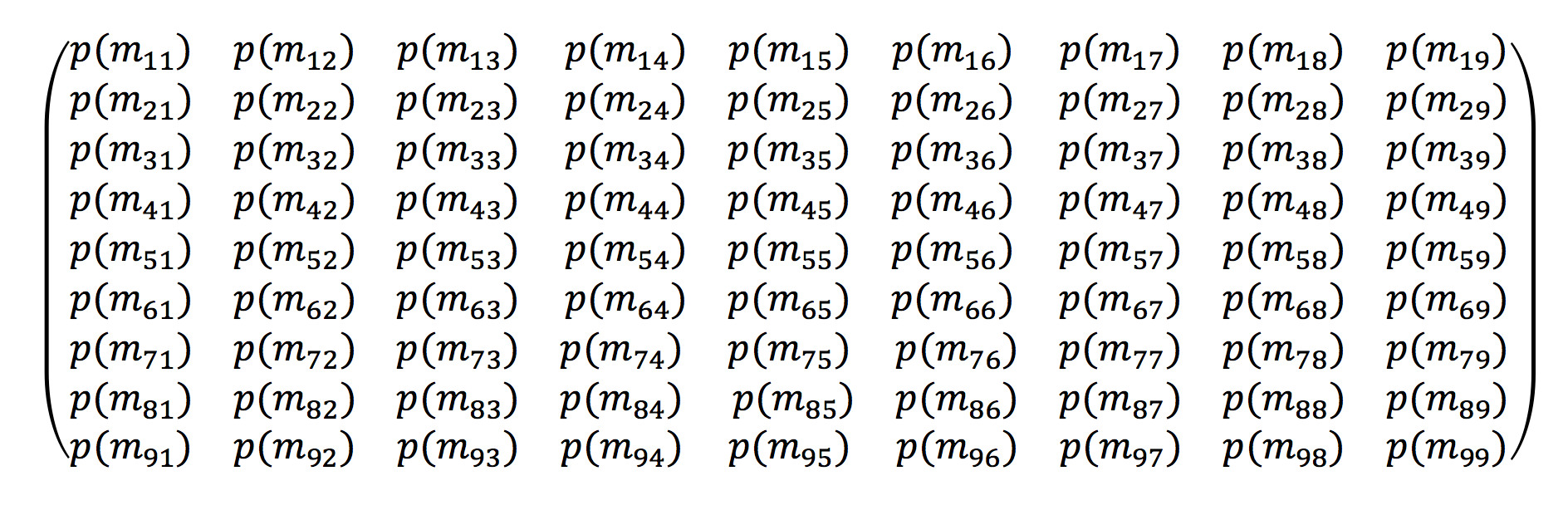
I now need to create a 9×9 matrix which represents all the states of the game.  The first subscript denotes where a player starts and the second subscript denotes where a player finishes after 1 turn.  So for example m_13 denotes that a player will start on square 1 and finish on square 3, and p(m_13) is the probability that it will happen.  If we do some (rather tedious!) calculations we get the following matrix:

We can note that the probability of ending up on square 5 is 0 because if you do land on it you are transported to Go.  Equally you can’t start on square 5 – so the probability of starting there and arriving somewhere else is also 0.  Also note that each row represents all possible states – so always adds up to 1.

Now all I need to do is raise this matrix to a large power.  If I raise this to the power 100 this will give me the long term probabilities of which square people will land on.  This will also give me a 9×9 matrix but I can focus on the first row which will tell me the long term probabilities of where people end up when starting at Go.  This gives:

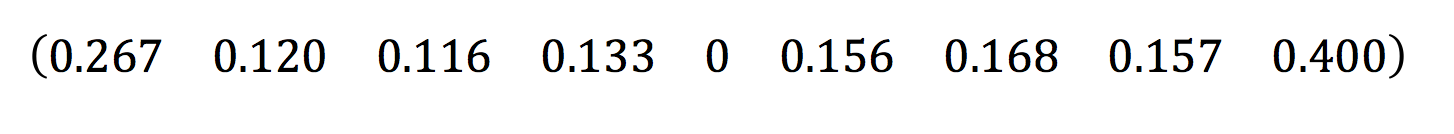
So I can see that the long term probabilities (to 3sf) show that Jail is going to be visited around 40% of the time, followed by Go (around 26.7% of the time).  And the mathematician that receives the most visits will be Euclid (around 16.8%).  We can logically see why this is true – if 40% of the time people are in Jail, then the next roll they are most likely to get a 7 which then takes them to this square.

Extensions

Clearly we can then refine our game – we could in theory use this to model the real game of Monopoly (though this would be quite complicated!)  The benefit of Markov chains is that it is able to reduce complex rules and systems into a simple long term probability – which is hugely useful for making long term predictions.