The Si(x) Function

A longer look at the Si(x) function

If you are a teacher then please also visit my new site: intermathematics.com for over 2000+ pdf pages of resources for teaching IB maths!

Sinx/x can’t be integrated into an elementary function – instead we define:

Where Si(x) is a special function.  This may sound strange – but we already come across another similar case with the integral of 1/x.  In this case we define the integral of 1/x as ln(x).  ln(x) is a function with its own graph and I can use it to work out definite integrals of 1/x.  For example the integral of 1/x from 1 to 5 will be ln(5) – ln(1) = ln(5).

The graph of Si(x) looks like this:

Or, on a larger scale:

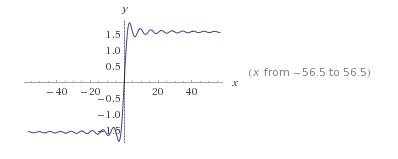
You can see that it is symmetrical about the y axis, has an oscillating motion and as x gets large approaches a limit.  In fact this limit is pi/2.

Because Si(0) = 0,  you can write the following integrals as:

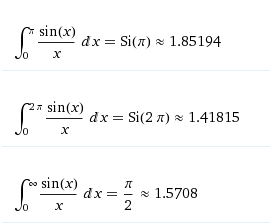
How to integrate sinx/x ?

It’s all very well to define a new function – and say that this is the integral of sinx/x – but how was this function generated in the first place?

Well, one way to integrate difficult functions is to use Taylor and Maclaurin expansions.  For example the Maclaurin expansion of sinx/x for values near x=0 is:

This means that in the domain close to x = 0, the function sinx/x behaves in a similar way to the polynomial above.  The last part of this expression O( )  just means everything else in this expansion will be x^6 or greater.

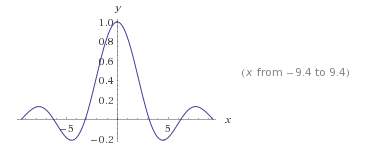
Graph of sinx/x

Graph of 1 – x^2/6 + x^4/120

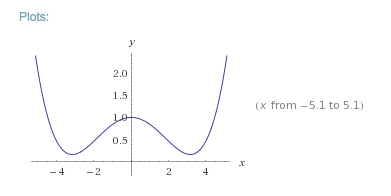
In the region close to x=0 these functions behave in a very similar manner (this would be easier to see with similar scales so let’s look on a GDC):

So for the region above (x between 0 and 2) the 2 graphs are virtually indistinguishable.

Therefore if we want to integrate sinx/x for values close to 0 we can just integrate our new function 1 – x^2/6 + x^4/120 and get a good approximation.

Let’s try how accurate this is.  We can use Wolfram Alpha to tell us that:

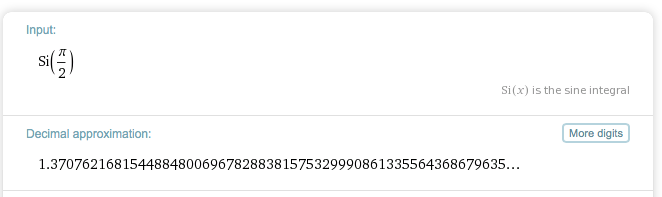
and let’s use Wolfram to work out the integral as well:

Our approximation is accurate to 3 dp, 1.371 in both cases.  If we wanted greater accuracy we would simply use more terms in the Maclaurin expansion.

So, by using the Maclaurin expansion for terms near x = 0 and the Taylor expansion for terms near x = a we can build up information as to the values of the Si(x) function.

Essential Resources for IB Teachers

1) Intermathematics.com

If you are a teacher then please also visit my new site.  This has been designed specifically for teachers of mathematics at international schools.  The content now includes over 2000 pages of pdf content for the entire SL and HL Analysis syllabus and also the SL Applications syllabus.  Some of the content includes:

1. Original pdf worksheets (with full worked solutions) designed to cover all the syllabus topics.  These make great homework sheets or in class worksheets – and are each designed to last between 40 minutes and 1 hour.
2. Original Paper 3 investigations (with full worked solutions) to develop investigative techniques and support both the exploration and the Paper 3 examination.
3. Over 150 pages of Coursework Guides to introduce students to the essentials behind getting an excellent mark on their exploration coursework.
4. A large number of enrichment activities such as treasure hunts, quizzes, investigations, Desmos explorations, Python coding and more – to engage IB learners in the course.

There is also a lot more.  I think this could save teachers 200+ hours of preparation time in delivering an IB maths course – so it should be well worth exploring!

Essential Resources for both IB teachers and IB students

1) Exploration Guides and Paper 3 Resources

I’ve put together a 168 page Super Exploration Guide to talk students and teachers through all aspects of producing an excellent coursework submission.  Students always make the same mistakes when doing their coursework – get the inside track from an IB moderator!  I have also made Paper 3 packs for HL Analysis and also Applications students to help prepare for their Paper 3 exams.  The Exploration Guides can be downloaded here and the Paper 3 Questions can be downloaded here.