IB Maths Resources from Intermathematics
IB Maths Resources: 300 IB Maths Exploration ideas, video tutorials and Exploration Guides
Cowculus - the farmer and the cow The Numberphile video linked the end of this is an excellent starting point for an investigation - so I thought I'd use this to extend the problem to a more general situation. The simple case is as follows: A farmer is at point F and a cow at... Continue Reading →
https://www.youtube.com/watch?v=rHdYv62F5fs The Perfect Rugby Kick This was inspired by the ever excellent Numberphile video which looked at this problem from the perspective of Geogebra. I thought I would look at the algebra behind this. In rugby we have the situation that when a try is scored, there is an additional kick (conversion kick) which can... Continue Reading →
Galileo's Inclined Planes This post is based on the maths and ideas of Hahn's Calculus in Context - which is probably the best mathematics book I've read in 20 years of studying and teaching mathematics. Highly recommended for both students and teachers! Hahn talks us though the mathematics, experiments and thought process of Galileo as... Continue Reading →
Complex Numbers as Matrices - Euler's Identity Euler's Identity below is regarded as one of the most beautiful equations in mathematics as it combines five of the most important constants in mathematics: I'm going to explore whether we can still see this relationship hold when we represent complex numbers as matrices. Complex Numbers as Matrices... Continue Reading →
Time dependent gravity and cosmology! In our universe we have a gravitational constant - i.e gravity is not dependent on time. If gravity changed with respect to time then the gravitational force exerted by the Sun on Earth would lessen (or increase) over time with all other factors remaining the same. Interestingly time-dependent gravity was... Continue Reading →
Projectiles IV: Time dependent gravity! This carries on our exploration of projectile motion - this time we will explore what happens if gravity is not fixed, but is instead a function of time. (This idea was suggested by and worked through by fellow IB teachers Daniel Hwang and Ferenc Beleznay). In our universe we... Continue Reading →
Projectile Motion III: Varying gravity We can also do some interesting things with projectile motion if we vary the gravitational pull when we look at projectile motion. The following graphs are all plotted in parametric form. Here t is the parameter, v is the initial velocity which we will keep constant, theta is the angle... Continue Reading →
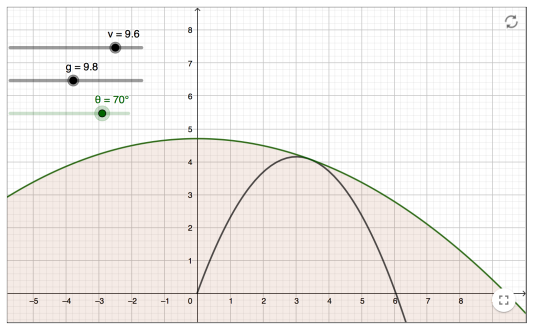
Projectile Motion Investigation II Another example for investigating projectile motion has been provided by fellow IB teacher Ferenc Beleznay. Here we fix the velocity and then vary the angle, then to plot the maximum points of the parabolas. He has created a Geogebra app to show this (shown above). The locus of these maximum points... Continue Reading →
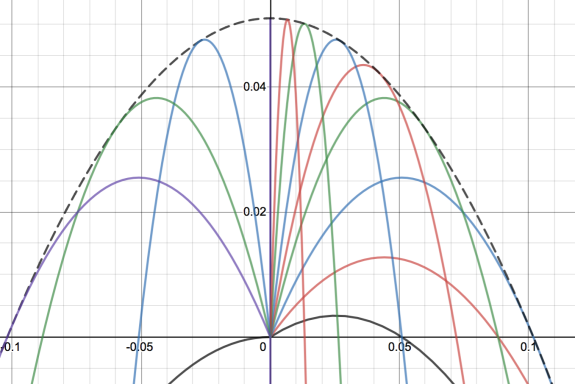
Envelope of projectile motion For any given launch angle and for a fixed initial velocity we will get projectile motion. In the graph above I have changed the launch angle to generate different quadratics. The black dotted line is then called the envelope of all these lines, and is the boundary line formed when I... Continue Reading →
https://www.youtube.com/watch?v=ZOiF7ZlboXA Rational Approximations to Irrational Numbers This year two mathematicians (James Maynard and Dimitris Koukoulopoulos) managed to prove a long-standing Number Theory problem called the Duffin Schaeffer Conjecture. The problem is concerned with the ability to obtain rational approximations to irrational numbers. For example, a rational approximation to pi is 22/7. This gives 3.142857 and... Continue Reading →
Soap Bubbles and Catenoids Soap bubbles form such that they create a shape with the minimum surface area for the given constraints. For a fixed volume the minimum surface area is a sphere, which is why soap bubbles will form spheres where possible. We can also investigate what happens when a soap film is formed... Continue Reading →
https://www.youtube.com/watch?v=5TkIe60y2GI Normal Numbers - and random number generators Numberphile have a nice new video where Matt Parker discusses all different types of numbers - including "normal numbers". Normal numbers are defined as irrational numbers for which the probability of choosing any given 1 digit number is the same, the probability of choosing any given 2... Continue Reading →
Cartoon from here The Gini Coefficient - Measuring Inequality The Gini coefficient is a value ranging from 0 to 1 which measures inequality. 0 represents perfect equality - i.e everyone in a population has exactly the same wealth. 1 represents complete inequality - i.e 1 person has all the wealth and everyone else has nothing.... Continue Reading →
Is Intergalactic space travel possible? The Andromeda Galaxy is around 2.5 million light years away - a distance so large that even with the speed of light at traveling as 300,000,000m/s it has taken 2.5 million years for that light to arrive. The question is, would it ever be possible for a journey to the... Continue Reading →
The Folium of Descartes The folium of Descartes is a famous curve named after the French philosopher and mathematician Rene Descartes (pictured top right). As well as significant contributions to philosophy ("I think therefore I am") he was also the father of modern geometry through the development of the x,y coordinate system of plotting algebraic... Continue Reading →
The Remarkable Dirac Delta Function This is a brief introduction to the Dirac Delta function - named after the legendary Nobel prize winning physicist Paul Dirac. Dirac was one of the founding fathers of the mathematics of quantum mechanics, and is widely regarded as one of the most influential physicists of the 20th Century. This... Continue Reading →
Maths of Global Warming - Modeling Climate Change The above graph is from NASA's climate change site, and was compiled from analysis of ice core data. Scientists from the National Oceanic and Atmospheric Administration (NOAA) drilled into thick polar ice and then looked at the carbon content of air trapped in small bubbles in the... Continue Reading →
A longer look at the Si(x) function Sinx/x can't be integrated into an elementary function - instead we define: Where Si(x) is a special function. This may sound strange - but we already come across another similar case with the integral of 1/x. In this case we define the integral of 1/x as ln(x). ln(x) is... Continue Reading →
This was the last question on the May 2016 Calculus option paper for IB HL. It's worth nearly a quarter of the entire marks - and is well off the syllabus in its difficulty. You could make a case for this being the most difficult IB HL question ever. As such it was a terrible exam... Continue Reading →
IB HL Calculus P3 May 2016: The Hardest IB Paper Ever? IB HL Paper 3 Calculus May 2016 was a very poor paper. It was unduly difficult and missed off huge chunks of the syllabus. You can see question 5 posted above. (I work through the solution to this in the next post). This is so... Continue Reading →
This is a nice example of using some maths to solve a puzzle from the mindyourdecisions youtube channel (screencaptures from the video). How to Avoid The Troll: A Puzzle In these situations it's best to look at the extreme case first so you get some idea of the problem. If you are feeling particularly pessimistic... Continue Reading →
https://www.youtube.com/watch?v=na6QspKHt48 Bullet Projectile Motion Experiment This is a classic physics experiment which counter to our intuition. We have a situation where 1 ball is dropped from a point, and another ball is thrown horizontally from that same point. The question is which ball will hit the ground first? (diagram from School for Champions site) Looking... Continue Reading →