Bullet Projectile Motion Experiment
This is a classic physics experiment which counter to our intuition. We have a situation where 1 ball is dropped from a point, and another ball is thrown horizontally from that same point. The question is which ball will hit the ground first?

(diagram from School for Champions site)
Looking at the diagram above you might argue that the ball that is dropped falls to the floor quicker as it has a shorter path. Or, you might think that the ball thrown sideways would travel faster to the ground because of its initial horizontal velocity. Both of these views are wrong however – as both balls will land at exactly the same time. To understand why, let’s look at the 2 situations in turn.
The ball launched sideways
To show that both balls would hit the ground at the same time we need to split the motion into its x and y components. We have
Where the angle theta is the angle of launch, v is the initial velocity, g is the gravitational constant 9.8 m/s. If we have a launch from the horizontal direction, then this angle is 0, which gives the simplified equations:
x = vt
y = 0.5gt2
if we relabel y as the vertical distance (d), then we have:

which is the time taken (ignoring air resistance etc) for an object launched horizontally to fall a distance d, where g is the gravitational constant 9.8 m/s.
So if we have a ball launched at a speed of 1 m/s from a height of 1m, it would hit the ground when:
t = (2/9.8)0.5 = 0.45 seconds
So we can use this value of t to see how far in the x direction it has travelled:
x = vt
x = 1(0.45)
x = 0.45m.
The ball dropped vertically
We still start with:
But this time we have no initial velocity as so we simply get:
x = 0
y = 0.5gt2
or as before, if we relabel y as the vertical distance (d), then we have:

So with a ball dropped from a height of 1m, it would also hit the ground when:
t = (2/9.8)0.5 = 0.45 seconds
But this time the distance in the x direction will of course be 0.
Showing this graphically
We can also show this graphically using the tracker software. This allows you to track the motion of objects in videos. So using the video above we can set the axis, and the height of the table

and then the motion capture software actually plots the parabola of the ball’s motion.

This first graph shows the change in the y direction with respect to time for the ball launched horizontally. We have large steps because the video was in super slow motion, so there were frames of very little movement. Nevertheless we can clearly see the general parabola, with equation:
y = -0.43x2 -1.2x + 107
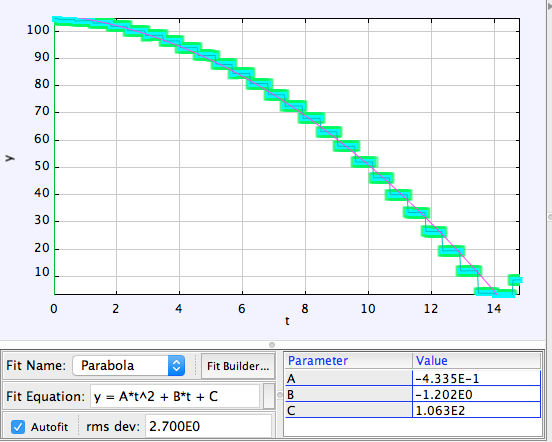
The second graph shows the change in y direction with respect to time for the ball dropped vertically down. As before we have a clear parabola, with equation:
y = -0.43x2 -1.2x + 106
Which is a remarkably close fit. So, there we go, we have shown that the vertical motion of our 2 objects are independent of their horizontal motion.
IB teacher? Please visit my new site http://www.intermathematics.com ! Hundreds of IB worksheets, unit tests, mock exams, treasure hunt activities, paper 3 activities, coursework support and more. Take some time to explore!
Are you a current IB student or IB teacher? Do you want to learn the tips and tricks to produce excellent Mathematics coursework? Check out my new IA Course in the menu!
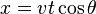

Is it “velocity in the y-direction” or “y-component of the velocity”? Just semantics, and I know we all say both, but is the first really valid? The velocity is a single vector: There are not two velocity vectors, each pointing in orthogonal directions.
Hi I would really appreciate it if you could help me with getting access to the motion capture software that you are using in this ME. Thanks a lot!