Graham’s Number – literally big enough to collapse your head into a black hole

Graham’s Number – literally big enough to collapse your head into a black hole

Graham’s Number is a number so big that it would literally collapse your head into a black hole were you fully able to comprehend it. And that’s not hyperbole – the informational content of Graham’s Number is so astronomically large that it exceeds the maximum amount of entropy that could be stored in a brain sized piece of space – i.e. a black hole would form prior to fully processing all the data content. This is a great introduction to notation for really big numbers. Numberphile have produced a fantastic video on the topic:

Graham’s Number makes use of Kuth’s up arrow notation (explanation from wikipedia:)

In the series of hyper-operations we have

1) Multiplication:

$\begin{matrix} a\times b & = & \underbrace{a+a+\dots+a} \\ & & b\mbox{ copies of }a \end{matrix}$

For example,

$\begin{matrix} 4\times 3 & = & \underbrace{4+4+4} & = & 12\\ & & 3\mbox{ copies of }4 \end{matrix}$

2) Exponentiation:

$\begin{matrix} a\uparrow b= a^b = & \underbrace{a\times a\times\dots\times a}\\ & b\mbox{ copies of }a \end{matrix}$

For example,

$\begin{matrix} 4\uparrow 3= 4^3 = & \underbrace{4\times 4\times 4} & = & 64\\ & 3\mbox{ copies of }4 \end{matrix}$

3) Tetration:

$\begin{matrix} a\uparrow\uparrow b & = {\ ^{b}a} = & \underbrace{a^{a^{{}^{.\,^{.\,^{.\,^a}}}}}} & = & \underbrace{a\uparrow (a\uparrow(\dots\uparrow a))} \\ & & b\mbox{ copies of }a & & b\mbox{ copies of }a \end{matrix}$

For example,

$\begin{matrix} 4\uparrow\uparrow 3 & = {\ ^{3}4} = & \underbrace{4^{4^4}} & = & \underbrace{4\uparrow (4\uparrow 4)} & = & 4^{256} & \approx & 1.34078079\times 10^{154}& \\ & & 3\mbox{ copies of }4 & & 3\mbox{ copies of }4 \end{matrix}$

$3\uparrow\uparrow 2=3^3=27$

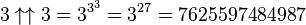
$3\uparrow\uparrow 3=3^{3^3}=3^{27}=7625597484987$

$3\uparrow\uparrow 4=3^{3^{3^3}}=3^{3^{27}}=3^{7625597484987}$

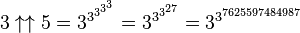
$3\uparrow\uparrow 5=3^{3^{3^{3^3}}}=3^{3^{3^{27}}}=3^{3^{7625597484987}}$

etc.

4) Pentation:

$\begin{matrix} a\uparrow\uparrow\uparrow b= & \underbrace{a_{}\uparrow\uparrow (a\uparrow\uparrow(\dots\uparrow\uparrow a))}\\ & b\mbox{ copies of }a \end{matrix}$

and so on.

Examples:

$3\uparrow\uparrow\uparrow2 = 3\uparrow\uparrow3 = 3^{3^3} = 3^{27}=7,625,597,484,987$

$\begin{matrix} 3\uparrow\uparrow\uparrow3 = 3\uparrow\uparrow3\uparrow\uparrow3 = 3\uparrow\uparrow(3\uparrow3\uparrow3) = & \underbrace{3_{}\uparrow 3\uparrow\dots\uparrow 3} \\ & 3\uparrow3\uparrow3\mbox{ copies of }3 \end{matrix} \begin{matrix} = & \underbrace{3_{}\uparrow 3\uparrow\dots\uparrow 3} \\ & \mbox{7,625,597,484,987 copies of 3} \end{matrix}=\underbrace{3^{3^{3^{3^{\cdot^{\cdot^{\cdot^{\cdot^{3}}}}}}}}}_{7,625,597,484,987}$

Which clearly can lead to some absolutely huge numbers very quickly. Graham’s Number – which was arrived at mathematically as an upper bound for a problem relating to vertices on hypercubes is (explanation from Wikipedia)

where the number of arrows in each layer, starting at the top layer, is specified by the value of the next layer below it; that is,

$G = g_{64},\text{ where }g_1=3\uparrow\uparrow\uparrow\uparrow 3,\ g_n = 3\uparrow^{g_{n-1}}3,$

and where a superscript on an up-arrow indicates how many arrows are there. In other words, G is calculated in 64 steps: the first step is to calculate g₁ with four up-arrows between 3s; the second step is to calculate g₂ with g₁ up-arrows between 3s; the third step is to calculate g₃ with g₂ up-arrows between 3s; and so on, until finally calculating G = g₆₄ with g₆₃ up-arrows between 3s.

So a number so big it can’t be fully processed by the human brain. This raises some interesting questions about maths and knowledge – Graham’s Number is an example of a number that exists but is beyond full human comprehension – it therefore is an example of a upper bound of human knowledge. Therefore will there always be things in the Universe which are beyond full human understanding? Or can mathematics provide a shortcut to knowledge that would otherwise be inaccessible?

IB teacher? Please visit my new site http://www.intermathematics.com ! Hundreds of IB worksheets, unit tests, mock exams, treasure hunt activities, paper 3 activities, coursework support and more. Take some time to explore!

― Andrew Chambers: (Resources for IB teachers)

Please visit the site shop: http://www.ibmathsresources.com/shop to find lots of great resources to support IB students and teachers – including the brand new May 2025 prediction papers.

― Andrew Chambers (Resources for Students)

Graham’s Number – literally big enough to collapse your head into a black hole

Like this:

Related

Leave a Reply

Share this:

Like this:

Related

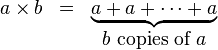
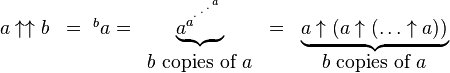
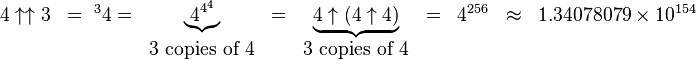
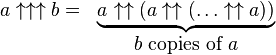
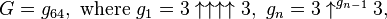
Leave a Reply