Hailstone Numbers

Hailstone Numbers

This is a post inspired by the article on the same topic by the ever brilliant Plus Maths. Hailstone numbers are created by the following rules:

if n is even: divide by 2

if n is odd: times by 3 and add 1

We can then generate a sequence from any starting number.  For example, starting with 10:

10, 5, 16, 8, 4, 2, 1, 4, 2, 1…

we can see that this sequence loops into an infinitely repeating 4,2,1 sequence.  Trying another number, say 58:

58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1…

and we see the same loop of 4,2,1.

In fact we can use the generator in the Plus Maths article to check any numbers we can think of, and we still get the pattern 4,2,1 looping.  The question is, does every number end in this loop?  Well, we don’t know.  Every number mathematicians have checked do indeed lead to this loop, but that is not a proof.  Perhaps there is a counter-example, we just haven’t found it yet.

Hailstone numbers are called as such because they fall, reach one (the ground) before bouncing up again.  The proper mathematical name for this investigation is the Collatz conjecture. This was made in 1937 by a German mathematian, Lothar Collatz.

One way to investigate this conjecture is to look at the length of time it takes a number to reach the number 1.  Some numbers take longer than others.  If we could find a number that didn’t reach 1 even in an infinite length of time then the Collatz conjecture would be false.

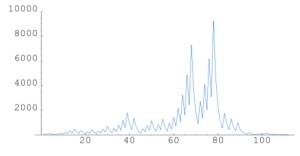
The following graphic from wikipedia shows how different numbers (x axis) take a different number of iterations (y axis) to reach 1.  We can see that some numbers take much longer than others to reach one.  For example, the number 73 has the following pattern:

73, 220, 110, 55, 166, 83, 250, 125, 376, 188, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1…

so investigating what it is about certain numbers that leads to long chains is one possible approach to solving the conjecture. This conjecture has been checked by computers up to a staggering 5.8 x 10¹⁸ numbers. That would suggest that the conjecture could be true – but doesn’t prove it is. Despite looking deceptively simple, Paul Erdos – one of the great 20th century mathematicians stated in the 1980s that “mathematics is not yet ready for such problems” – and it has remained unsolved over the past few decades.  Maybe you could be the one to crack this problem!

If you liked this post you might also like:

Friendly Numbers, Solitary Numbers, Perfect Numbers – a look at some other number sequence problems.