IB Maths Resources from Intermathematics
IB Maths Resources: 300 IB Maths Exploration ideas, video tutorials and Exploration Guides
Cowculus - the farmer and the cow The Numberphile video linked the end of this is an excellent starting point for an investigation - so I thought I'd use this to extend the problem to a more general situation. The simple case is as follows: A farmer is at point F and a cow at... Continue Reading →
https://www.youtube.com/watch?v=4dyytPboqvE This year's TOK question for Mathematics is the following: "How can we reconcile the opposing demands for specialization and generalization in the production of knowledge? Discuss with reference to mathematics and one other area of knowledge" This is a nice chance to discuss the Langlands program which was recently covered in a really excellent... Continue Reading →
Toads and snakes: an investigation! We have 2 populations: Toads who live inside a circle (a pond) and snakes which live inside a square (field). If the circle is completely surrounded by the square then no toads can live, and if the square is completely surrounded by the circle, no snakes can live. We want... Continue Reading →
https://www.youtube.com/watch?v=rHdYv62F5fs The Perfect Rugby Kick This was inspired by the ever excellent Numberphile video which looked at this problem from the perspective of Geogebra. I thought I would look at the algebra behind this. In rugby we have the situation that when a try is scored, there is an additional kick (conversion kick) which can... Continue Reading →
Prime Spirals - Patterns in Primes One of the fundamental goals of pure mathematicians is gaining a deeper understanding of the distribution of prime numbers - hence why the Riemann Hypothesis is one of the great unsolved problems in number theory and has a $1 million prize for anyone who can solve it. Prime numbers... Continue Reading →
The Barnsley Fern: Mathematical Art This pattern of a fern pictured above was generated by a simple iterative program designed by mathematician Michael Barnsely. I downloaded the Python code from the excellent Tutorialspoint and then modified it slightly to run on repl.it. What we are seeing is the result of 40,000 individual points - each plotted... Continue Reading →
Sphere packing problem: Pyramid design Sphere packing problems are a maths problems which have been considered over many centuries - they concern the optimal way of packing spheres so that the wasted space is minimised. You can achieve an average packing density of around 74% when you stack many spheres together, but today I want to... Continue Reading →
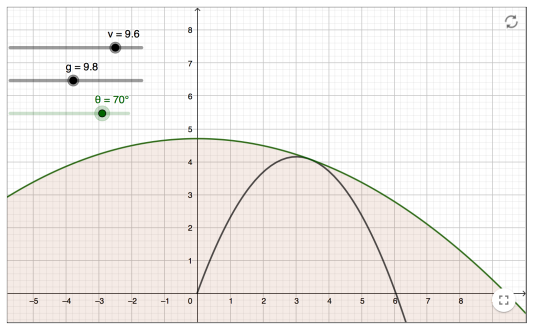
Projectile Motion III: Varying gravity We can also do some interesting things with projectile motion if we vary the gravitational pull when we look at projectile motion. The following graphs are all plotted in parametric form. Here t is the parameter, v is the initial velocity which we will keep constant, theta is the angle... Continue Reading →
Projectile Motion Investigation II Another example for investigating projectile motion has been provided by fellow IB teacher Ferenc Beleznay. Here we fix the velocity and then vary the angle, then to plot the maximum points of the parabolas. He has created a Geogebra app to show this (shown above). The locus of these maximum points... Continue Reading →
https://www.youtube.com/watch?v=1EkoaQJyrfk Classical Geometry Puzzle: Finding the Radius This is another look at a puzzle from Mind Your Decisions. The problem is to find the radius of the following circle: We are told that line AD and BC are perpendicular and the lengths of some parts of chords, but not much more! First I'll look at... Continue Reading →
When do 2 squares equal 2 cubes? Following on from the hollow square investigation this time I will investigate what numbers can be written as both the sum of 2 squares, 2 cubes and 2 powers of 4. i.e a2+b2 = c3+d3 = e4+f4. Geometrically we can think of this as trying to find an... Continue Reading →
Ramanujan's Taxi Cabs and the Sum of 2 Cubes The Indian mathematician Ramanujan (picture cite: Wikipedia) is renowned as one of great self-taught mathematical prodigies. His correspondence with the renowned mathematician G. H Hardy led him to being invited to study in England, though whilst there he fell sick. Visiting him in hospital, Hardy remarked that... Continue Reading →
The Shoelace Algorithm to find areas of polygons This is a nice algorithm, formally known as Gauss's Area formula, which allows you to work out the area of any polygon as long as you know the Cartesian coordinates of the vertices. The case can be shown to work for all triangles, and then can be... Continue Reading →
Soap Bubbles and Catenoids Soap bubbles form such that they create a shape with the minimum surface area for the given constraints. For a fixed volume the minimum surface area is a sphere, which is why soap bubbles will form spheres where possible. We can also investigate what happens when a soap film is formed... Continue Reading →
https://www.youtube.com/watch?v=FFftmWSzgmk Plotting the Mandelbrot Set The video above gives a fantastic account of how we can use technology to generate the Mandelbrot Set - one of the most impressive mathematical structures you can imagine. The Mandelbrot Set can be thought of as an infinitely large picture - which contains fractal patterns no matter how far... Continue Reading →
https://www.youtube.com/watch?v=0hlvhQZIOQw This carries on the previous investigation into Farey sequences, and is again based on the current Nrich task Ford Circles. Below are the Farey sequences for F2, F3 and F4. You can read about Farey sequences in the previous post. This time I'm going to explore the link between Farey sequences and circles. First... Continue Reading →
The Folium of Descartes The folium of Descartes is a famous curve named after the French philosopher and mathematician Rene Descartes (pictured top right). As well as significant contributions to philosophy ("I think therefore I am") he was also the father of modern geometry through the development of the x,y coordinate system of plotting algebraic... Continue Reading →
https://www.youtube.com/watch?v=KfAs2hztDtI Measuring the Distance to the Stars This is a very nice example of some very simple mathematics achieving something which for centuries appeared impossible - measuring the distance to the stars. Before we start we need a few definitions: 1 Astronomical Unit (AU) is the average distance from the Sun to the Earth. This... Continue Reading →
This post is inspired by the Quora thread on interesting functions to plot. The butterfly This is a slightly simpler version of the butterfly curve which is plotted using polar coordinates on Desmos as: Polar coordinates are an alternative way of plotting functions - and are explored a little in HL Maths when looking at... Continue Reading →
Euler's 9 Point Circle This is a nice introduction to some of the beautiful constructions of geometry. This branch of mathematics goes in and out of favour - back in the days of Euclid, constructions using lines and circles were a cornerstone of mathematical proof, interest was later revived in the 1800s through Poncelot's projective... Continue Reading →