IB Maths Resources from Intermathematics
IB Maths Resources: 300 IB Maths Exploration ideas, video tutorials and Exploration Guides
Projectiles IV: Time dependent gravity! This carries on our exploration of projectile motion - this time we will explore what happens if gravity is not fixed, but is instead a function of time. (This idea was suggested by and worked through by fellow IB teachers Daniel Hwang and Ferenc Beleznay). In our universe we... Continue Reading →
Projectile Motion III: Varying gravity We can also do some interesting things with projectile motion if we vary the gravitational pull when we look at projectile motion. The following graphs are all plotted in parametric form. Here t is the parameter, v is the initial velocity which we will keep constant, theta is the angle... Continue Reading →
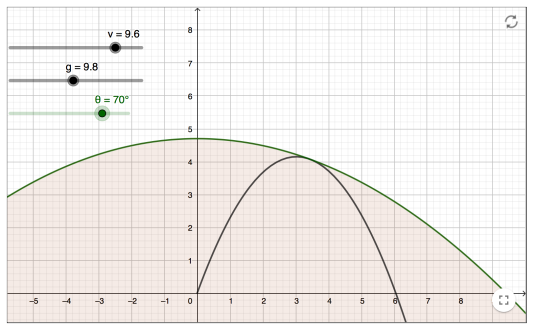
Projectile Motion Investigation II Another example for investigating projectile motion has been provided by fellow IB teacher Ferenc Beleznay. Here we fix the velocity and then vary the angle, then to plot the maximum points of the parabolas. He has created a Geogebra app to show this (shown above). The locus of these maximum points... Continue Reading →
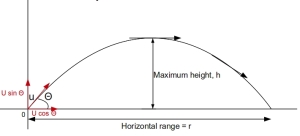
War Maths - Projectile Motion Despite maths having a reputation for being a somewhat bookish subject, it is also an integral part of the seamier side of human nature and has been used by armies to give their side an advantage in wars throughout the ages. Military officers all need to have a firm grasp... Continue Reading →