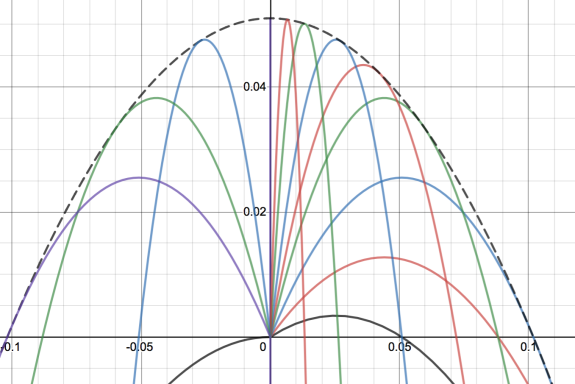
Envelope of projectile motion For any given launch angle and for a fixed initial velocity we will get projectile motion. In the graph above I have changed the launch angle to generate different quadratics.  The black dotted line is then called the envelope of all these lines, and is the boundary line formed when I... Continue Reading →